[Adobe Animate CC使い方講座] HTML5 canvasとAIRモードの違いについて!
Adobe Animate CCには二つのモードがある!HTML5 canvasとAIRモードって何かを解説します。
前回の講座ではAdobe Animate CCがどのような経緯で生まれたのかを説明させて頂きました。今回はそれをふまえて、Adobe Animate CCの作成モードについて説明したいと思います。Adobe Animate CCは使いこなせれば、ものすごい力を持ったツールです。しかし、過去の経緯などもあって、そのモードや機能が複雑になってしまっている面があります。そういった難しい部分/用語をまず解説していきます。
まずはじめに戸惑うのがファイルの新規作成のモードです。下記のようにAdobe Animate CCにはたくさんの作成モードがあります。しかし、はじめてAdobe Animate CCを触る人にとっては、意味がわかりにくく、嫌がらせでしかありません。ここについて解説していきたいと思います。
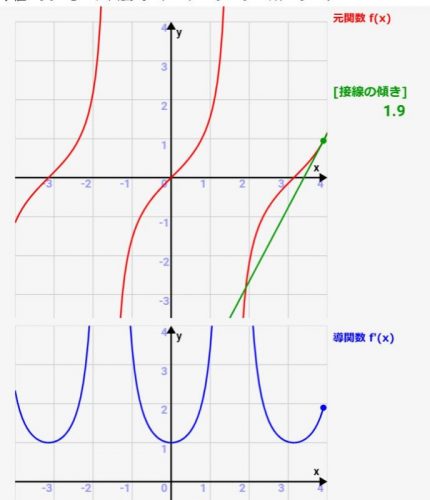
微分シミュレーター:三角関数(tan)の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
cosθとsinθの関係をアニメーションで理解しよう![数学入門]
このページでは簡単に数学の関数の一つである三角関数(sin,cos)を解説していきます。三角関数にはcos/sin/tanの3つがありますが、この中でもcosとsinの関係はとても強いです。
今回はこのcos/sinと単位円の関係をアニメーションで超分かりやすく示したいと思います!
![cosθとsinθの関係をアニメーションで理解しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20201213181737-500x495.jpg)
微分シミュレーター:三角関数(sin,cos)の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
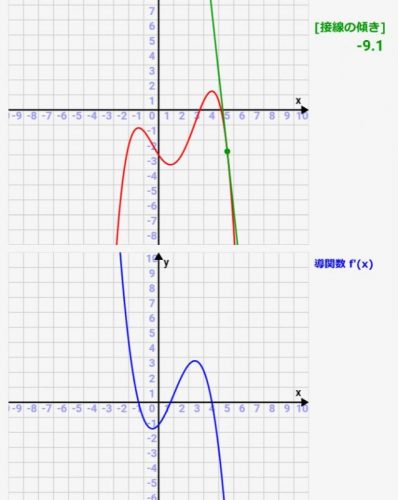
微分シミュレーター:四次関数の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
微分は、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
微分(導関数)の求め方/考え方については、コチラの記事で詳しく説明していますので、まずはそちらをご参照願います。