偏差値とは何か?をシミュレーターを用いて詳しく解説!実際に値入力して動きを確かめよう![統計学/確率入門]
本サイトでは、数学分野の内容を基礎から分かりやすくシミュレーターを用いて解説しています!このベースを用いて、以後「統計学/確率」の分野の内容を同様にシミュレーターを作って解説していきたいと思います!
よくテストの結果などで、「偏差値」を目にしますよね。偏差値50だったら普通で、偏差値70だとかなり良くて、偏差値40だとちょっとダメな結果、、、そんなイメージを持っていると思います。でも、偏差値の計算方法って良くわからないですよね。
ということで、前回までに説明した「標準偏差」の考え方を用いて、「偏差値」とは何かを本記事では解説していきます!実際にデータを入力して偏差値をリアルタイムに計算できるシミュレーターもありますので、それを使って色々実験してみて下さい!きっとイメージがつかめると思います!
![偏差値とは何か?をシミュレーターを用いて詳しく解説!実際に値入力して動きを確かめよう![統計学/確率入門]](https://retu27.com/wp-content/uploads/rapture_20200629223504-500x253.jpg)
目次
どのくらいテストの点数が凄いかは、「平均値」と「結果のバラツキ具合」で決まる
今回も例により0~100点のテストの結果を例にして考えていきます!
以下の2パターンの例を比較して考察します。両方とも平均値50点のテストであり、紫丸がその中での65点の結果です。いきなりですが、この2つの結果、どちらが凄いと思いますか??
普通に考えると、パターン1の前者ですよね。もちろんランク付けして順位が高いというのもそうですが、、、前者は50周辺で結果が集まっているのに、後者はかなりバラついています。とすると、「バラつきが少ない中で良い点数をとったほうが、より凄い」と言えるわけです!同じ点数、同じ平均点でもデータのバラツキによってテスト結果のスゴさが変わるわけです。
データの「バラつき」を表す「標準偏差」のおさらい
上記で言及したデータのバラつき、前回記事でそれを数値化する代表値として「分散」と「標準偏差」を紹介/解説しました。
ここで軽く復習しておきます。データのバラつき度合いは、下図の紫矢印で示している「平均値と各データ値の差異」で表せると言えます。バラつくほど、この差異が大きくなるはずなので。

そして、この長さを少し変形して計算したのが「標準偏差」です。
↓このように記号を定義すると、、、
- n: テストを受けた人数(データ個数)
- \(x_i\): i番目の人の点数
- \(\bar x \): 平均値
標準偏差は以下の式で表す事ができます。
\( 標準偏差σ \)
\( \displaystyle = \sqrt{\frac{1}{n}\sum_{i=1}^{n} (\bar x – x_i)^2} \)
標準偏差は図で表すと↓の緑色部分の長さになります。この標準偏差は、「平均値(赤線)と各データとの差異」の平均値であるとも言えます。
この標準偏差がデータのバラつきを表す指標として最適と言えます!
↓各得点データは、平均すると緑線の範囲ぐらい赤線から離れてる。この範囲が標準偏差です。
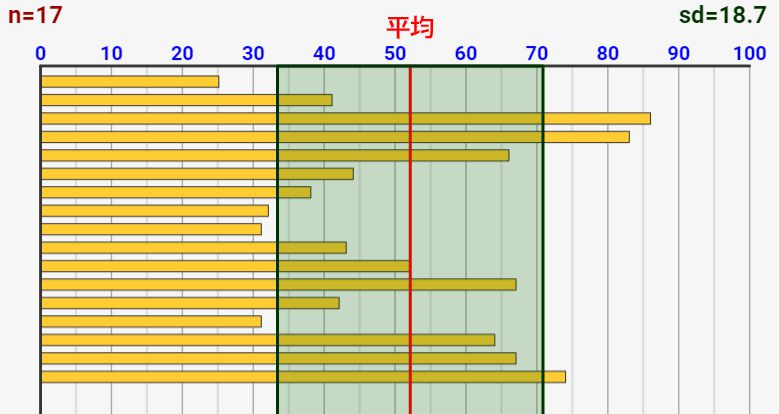
「偏差値」は標準偏差を少し変形しただけの指標値!
偏差値の定義
上記で説明した「標準偏差」を用いて、各テストの結果をわかりやすい指標に数値化するのが「偏差値」という考えです。
偏差値の考え方は以下の通りです。
・平均値の点数を基準点として、偏差値50とする
・標準偏差の長さ=10とみなして、偏差値からの差異で評価する
とりあえず平均値を50とランク付けして、標準偏差だけ離れていたら±10するという考え方です!
これを式で表すと
偏差値
\( \displaystyle = (\frac{テスト結果x_i – 平均値\bar x}{標準偏差σ}) × 10 + 50 \)
となります。これが偏差値の定義です!
偏差値の具体例
少し分かりにくいので、下記の例で考えてみます。
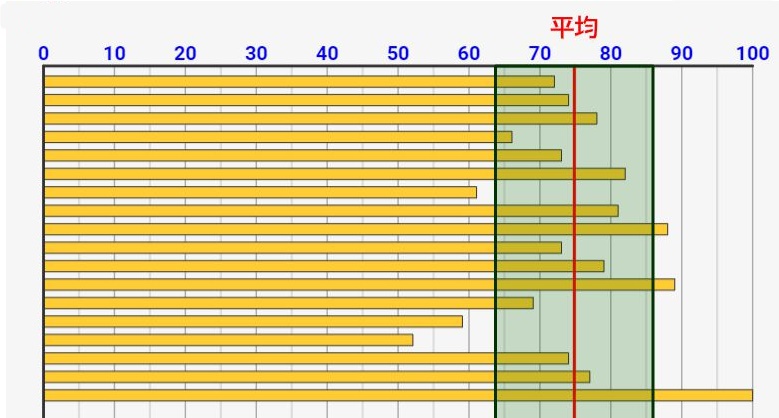
このとき、各値の偏差値は下図の通りになります。平均値(75点)を偏差値50とし、そこから標準偏差だけ足したとこ(緑色部分の一番上)を偏差値60、そこから標準偏差だけ引いたところ(緑色部分の一番下)を偏差値40とするわけです!図にすると凄く単純ですね!
あとは、この基準で各点数を偏差値に変換していけば良いだけです。バラつきが少ないほど標準偏差の長さが狭まるので、少しの差異で偏差値が大きく変わるようになります!
偏差値60 = 「標準偏差」分だけ平均より高いライン
自分でシミュレーターに点数を入力していき、偏差値の変動のイメージを掴もう!
シミュレーターの概要
ここまで解説した内容で分散と偏差値の定義は理解できたと思います。しかし、実際にどんな変動になるのかイメージがつきにくいですよね><
そこで、数値(テスト点数)を入力すると、リアルタイムに標準偏差の範囲を図示するシミュレーターを作りました!
今回もテストの結果を仮定して、0~100点までで値を入力できるようになっています。
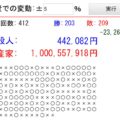
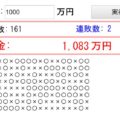
入力したテスト点数により、平均値(赤線)と標準偏差の範囲(緑枠)をリアルタイムに算出して表示します。平均値が偏差値50になり、緑色の上限が偏差値60、緑色の下限が偏差値40のラインになります。
更に黄色枠線が標準偏差×2の範囲を示しています。ですので、この黄色枠の上限が偏差値70、下限が偏差値30のラインを示します。
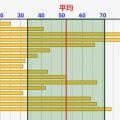
↓シミュレーターのスクリーンショット。こんな感じで平均値/標準偏差などを出力します
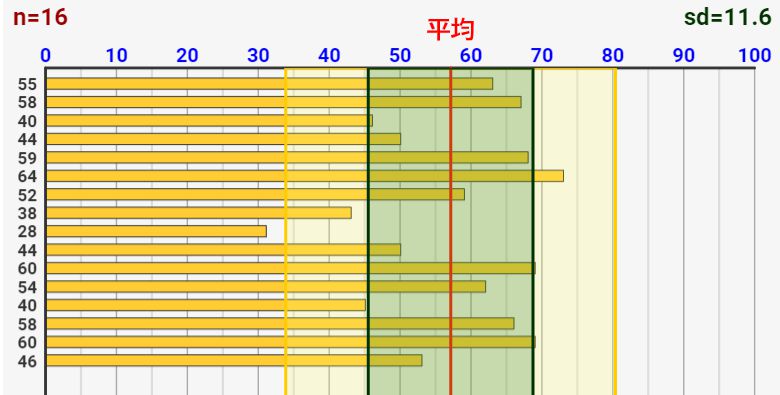
さらに重要なのが、左側の小さな数字。これは各テスト結果の偏差値を示しています!テスト結果を追加するたびに、平均値/標準偏差が変わり、変化していきます。
偏差値計算シミュレーターを実際に動かしてみよう!
実際にシミュレーターで実験してみましょう!
- スライドバーを動かすと、指/マウスを離した時点でその点数が追加されます
- データをどんどん入力・追加していき、平均値/標準偏差/各テスト結果の偏差値の変動を確かめて見ましょう
- リセットで初期化できます
- 右上のsdという値が実際の標準偏差の値です
データをバラついて配置すると標準偏差は広がり、極端な偏差値は出にくくなります。良い点数をとることが、ある意味当たり前になっていくからです。
それに対して、ほとんど分散させずに点数を配置していくと、少しでも大きな点数を配置した瞬間に偏差値80といった大きな値が出ます。皆からかけ離れた高い点数をとっている→高い偏差値となる訳です!
テストの結果は点数だけでは評価できない。だからこそ、偏差値が必要!
本記事では「偏差値」について、シミュレーターを用いて詳しく説明しました。偏差値は、どれだけそのテストの結果が凄いかを表す数値です。
一般的に、テストの点数だけではスゴさは評価できません。テストの点数40点でも、他の人が20点しか取れていなかったら凄く良い結果と言えますし、データのバラツキ具合によってもスゴさが変わってきます。
これに対して、平均値/データのバラつき(標準偏差)を用いて、50を基準としてテスト結果を評価するのが偏差値です!これによって、どれぐらい突出した素晴らしいい点数なのかが簡単に数値化出来るわけです!
普段見慣れている偏差値ですが、自分で計算することはあまりないと思うので、上のシミュレーターでイメージを掴んでおきましょう!
- まずは平均値を基準の50とする
- バラつきの指標である「標準偏差」の長さを10と換算して点数化したもの
- 例えば偏差値40 は「標準偏差」分だけ平均より低いライン、差値60 は「標準偏差」分だけ平均より高いラインとなる
⇒「平均/分散等の代表値」カテゴリ記事一覧
その他関連カテゴリ