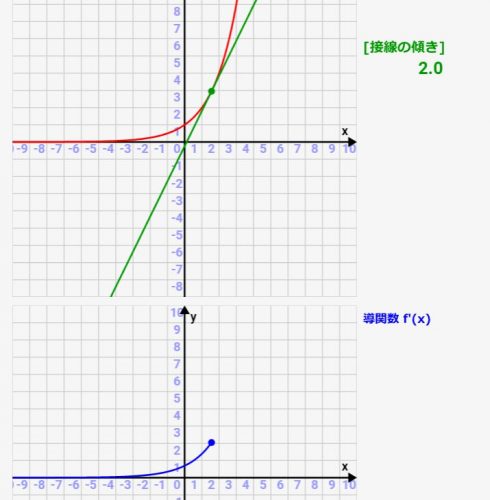
微分シミュレーター:三角関数(tan)の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
微分シミュレーター:三角関数(sin,cos)の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
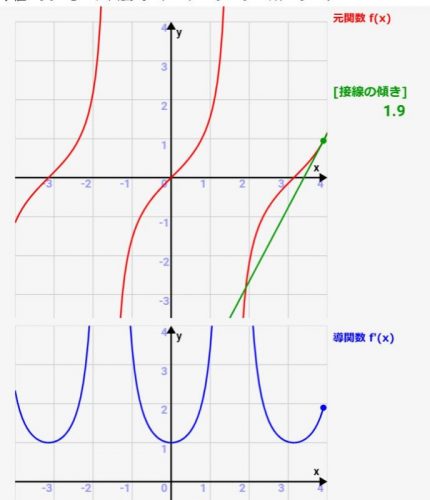
微分シミュレーター:四次関数の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
微分は、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
微分(導関数)の求め方/考え方については、コチラの記事で詳しく説明していますので、まずはそちらをご参照願います。
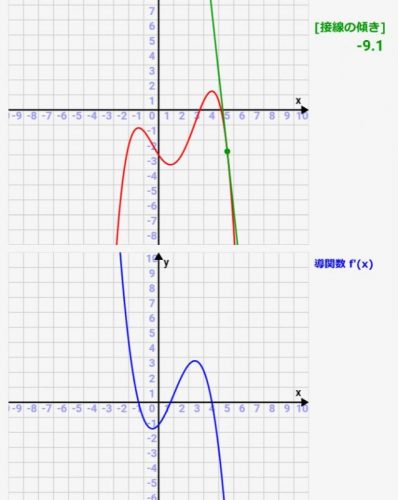
微分シミュレーター:三次関数の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
微分(導関数)の求め方/考え方については、コチラの記事で詳しく説明していますので、まずはそちらをご参照願います。
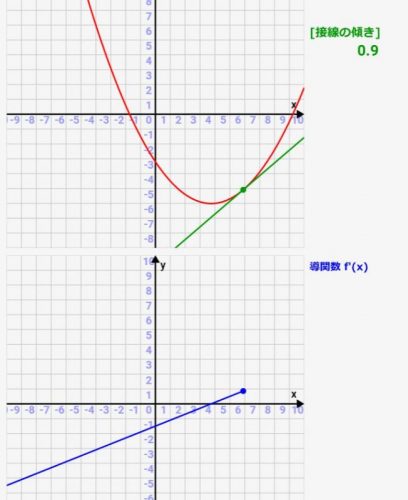
微分シミュレーター:指数関数の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!