等比数列をシミュレーション/図解で理解![数学入門]
本記事では「等比数列」について詳しく説明していきます。数列とは、「数が順番にならんだもの」を意味します。例として「1,7,5,3,12」「3,6,9,2,11」などが挙げられます。この中で、各数字の差が等しいものを等差数列と言います。この等差数列については、前回記事で詳しく説明してますので参照下さい。
そして、今回説明する等比数列とは、「隣同士の数の比が同じもの」の事を言います。
![等比数列をシミュレーション/図解で理解![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200505211046-283x500.jpg)
微分シミュレーター:指数関数の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
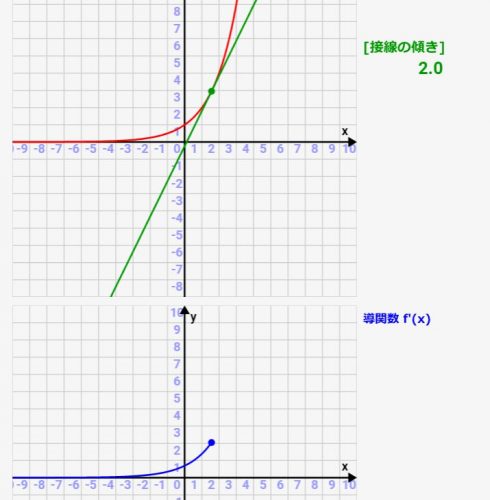
微分シミュレーター:対数関数の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
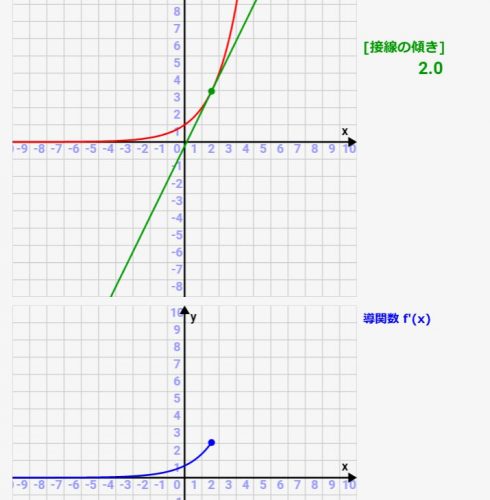
微分シミュレーター:二次関数の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
微分(導関数)の求め方/考え方については、コチラの記事で詳しく説明していますので、まずはそちらをご参照願います。
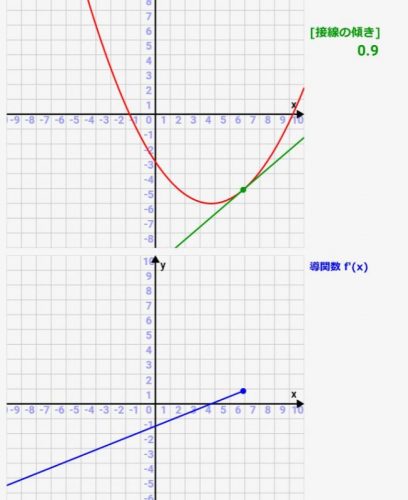
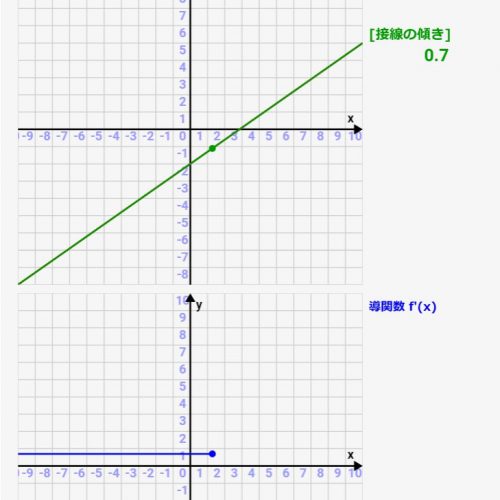
微分シミュレーター:一次関数の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
微分(導関数)の求め方/考え方については、コチラの記事で詳しく説明していますので、まずはそちらをご参照願います。