等比数列をシミュレーション/図解で理解![数学入門]
本記事では「等比数列」について詳しく説明していきます。数列とは、「数が順番にならんだもの」を意味します。例として「1,7,5,3,12」「3,6,9,2,11」などが挙げられます。この中で、各数字の差が等しいものを等差数列と言います。この等差数列については、前回記事で詳しく説明してますので参照下さい。
そして、今回説明する等比数列とは、「隣同士の数の比が同じもの」の事を言います。
![等比数列をシミュレーション/図解で理解![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200505211046-283x500.jpg)
目次
等比数列とは?
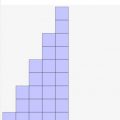
例えば↓が等比数列の例です。この数列は隣同士で2倍になってますよね。つまり、隣同士の比が2で固定。なのでこれは等比数列と言えます!
↓図で表すとこんな感じ。等比数列は比が同じなので指数関数的な形状になります

等比数列の用語
ここで等比数列を表す時に必要な用語の説明をします。一部は等差数列と同じですね。
初項は最初の数を意味します。つまり、一番左側の数ですね。そして交比は各数の比です。つまり上の例では、初項が3で公比が2の等比数列と言えます。
大事なのは、等差数列と同じく、初項と公比の2つが決まれば全ての項が表せるということです。最初の数と、それ以後の数の比がわかれば、以後の数が全て決まりますから。
その他の等比数列の例
その他2つ、等比数列の例を説明します。
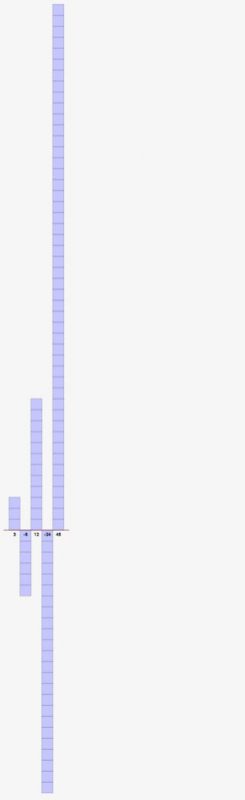
↓コチラも同じく等差数列になります。比は2ですね。初項がマイナスなので、マイナス方向に突き進んでいきます。
\( -2,-4,-8,-16,-32 \)
↓こちらも同じく等比数列です。各項、正数と負数が交互に出てきていますが、これは公比が-2だからです。公比がマイナスになると、各項はプラス/マイナスの繰り返しとなります。
\( 3,-6,12,-24,48 \)
上記のような等差数列を一般化すると、等差数列のn番目の要素a_nは次のように書けます。
等比数列の一般表記
上でいくつか例に挙げた等比数列は以下の表記で定義できます。
* \(a_1\): 初項
\(r\): 交比(各項の比)
等比数列は、初項に交比(各項の比)をn-1個乗算することで各項を計算できるというわけです。各nで値を当てはめてみると分かりやすいです。1つ目は\(a_1\)で、2つ目は\(a_1 \cdot r \)、3つ目が\(a_1 \cdot r^2 \)と表せます。\(a_1\)から始まり、\(r\)がその後一つずつ乗算されていく感じです。
等比数列をシミュレーションで理解しよう!
今まで説明した等比数列をさらにイメージしやすくするため、シミュレーターを作成しました。自分で値を指定し、等比数列のイメージ図を作ってみましょう!
- 初項(\(a_1\))、交比(\(r\))、項数(\(n\))を指定すると、数列をブロック形式で図示してくれます
- 値を変えると再描画するので、色々値を変えてイメージを掴みましょう
等比数列の和を計算してみる!
それでは、上記の等比数列の総和を考えてみます。イメージとしては上記のブロック数を全て数えれば良いことになります(マイナス分は引く)。
等差数列と違ってこれは工夫が必要です。そのままだと計算しにくいので、、、ちょっとしたテクニックを使います。
今、初項1、公比2の簡単な等比数列を考えます。図で見ると↓のような感じ。
これに対して、全体にr=2をかけた数列を考えてみます。
この2つ、比べると最初と最後の項以外重複しているんです。↓の紫部分が重複しているところ。完全に一致してますね。
何故なら、
\(a_{n} = \displaystyle a \cdot r^{n-1} \)
\(r \cdot a_{n} = \displaystyle a \cdot r^{n} \)
となり、「1)元の等比数列の\(a_{n}\)=2)r乗算した等比数列の\(a_{n-1}\)」という式が成り立つからです。そのため、等比数列の合計を\(S_n\)として、上記2つの数列の差\(r \cdot S_n – S_n \)をとると、2)の最後の項と1)の最初の項しか残らないんです!
\(= \displaystyle a \cdot r^{n} – a \)
\(r \cdot S_n – S_n = (r-1)S_n \)であり、 \(a \cdot r^{n} – a = a(r^{n} – 1) \)であるため、これを変形すると
となります。マジックみたいですが、これで等比数列の合計\( S_n \)が求まります!
ちなみにr=1の時には上記式は使えません。ただr=1ということは、公比が1になるので\(a_n=a_1\)といえるため、
と単純に計算出来ます
このイメージをつけるために、この計算過程をシミュレーション化してみました!
等比数列の和の計算を、シミュレーターで理解しよう!
上記の等比数列の総和を計算するイメージをシミュレーションできます。↓の初項\(a_1\)/交比r/項数nを変えるとシミュレーションが動きます!シミュレーションでは以下の2つを図示します。
\(a_{n} = \displaystyle a \cdot r^{n-1} \)
\(a_{n} = \displaystyle a \cdot r^{n} \)
シミュレーション過程は上記の通り、1)元の等比数列を図示、2)それにrを乗算した数列を図示、3)両方の差をとって最初の項と最後の項が残るのを確かめる、4)最後に上記数式に当てはめて総和\(S_n\)を計算、という流れになります。
- 等比数列は一定の比率で伸びていく数列
- 等比数列の合計値は面積の引き算でうまく求められる
⇒「数列」カテゴリ記事一覧
その他関連カテゴリ