Cloudflareなら、ほぼ無料で独自ドメインメール運用可能!
独自ドメインメール、、、普通にやったら1000円以上かかってしまう
独自ドメインメールとはtest@retu27.comというように、自分のドメインを使ったメルアドのことです。gmailなどでなく、無料ドメインのアドレスよりも、信用性が増すと言われてます。
この独自ドメインメールですが、普通に取得しようとすると結構ややこしいです。また、結構料金がかかったりします。
例えばgmailで独自ドメインのメールを紐づけしようとすると、GSuiteサービスに入会せねばならず、↓のような料金がかかってしまいます。

WebArena各サービスがが値上げ…他サービスに移行します
お気に入りだったWebArena
本サイトは2018年からWebArena VPSに移動して運用してきました。
このWebArena VPS、非常にネットワーク性能がよく、4000円超えと多少高めだったのですが満足して使っていました。
他のサイトが100Mbpsが限界になっているのに、WebArenaだけは800Mbpsとか出てたんですよね。
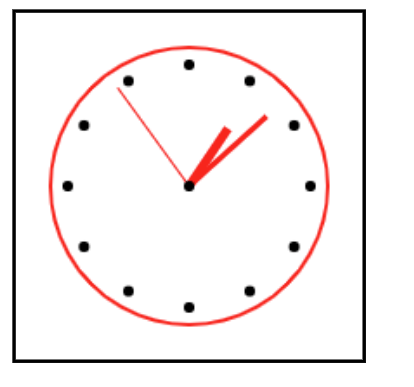
ChatGPT 自動プログラミング実験: 「アナログ時計」を作らせてみた!
自分が今まで理系の学問系中心に、内容を深く理解するためのシミュレータープログラムを作成してきました。このシミュレーター、簡単なものなら結構短いプログラムで書けてしまうこともあります。
「それなら、ChatGPTに全てプログラムを書かせるのも有り?」とふと思いました。ということで、様々なブラウザで動くようなシミュレーターやゲームをChatGPTに作成させる実験をしていきたいと思っています!
ChatGPT 自動プログラミング実験: 「ライフゲーム」を作らせてみた!
自分が今まで理系の学問系中心に、内容を深く理解するためのシミュレータープログラムを作成してきました。このシミュレーター、簡単なものなら結構短いプログラムで書けてしまうこともあります。
「それなら、ChatGPTに全てプログラムを書かせるのも有り?」とふと思いました。ということで、様々なブラウザで動くようなシミュレーターやゲームをChatGPTに作成させる実験をしていきたいと思っています!

ChatGPT 自動プログラミング実験: 「サイコロ シミュレーター」を作らせてみた!
自分が今まで理系の学問系中心に、内容を深く理解するためのシミュレータープログラムを作成してきました。このシミュレーター、簡単なものなら結構短いプログラムで書けてしまうこともあります。
「それなら、ChatGPTに全てプログラムを書かせるのも有り?」とふと思いました。ということで、様々なブラウザで動くようなシミュレーターやゲームをChatGPTに作成させる実験をしていきたいと思っています!