微分シミュレーター:三角関数(sin,cos)の微分!関数とその導関数(微分)の関係をアニメーションで確認可!
高校で習う微分、公式は習うのですが、実際にどういった関数グラフになっているかとか、元の関数との関係性が分かりにくかったりしますよね><
微分(導関数)は「元の関数の各点での接線の傾き」を表したものです。ですので、元の関数の接線を描き、その傾きをグラフ化すれば微分(導関数)になっているんです!その関係性がわかるような、シミュレーターを実際に作ってみました!パラメタを変えると、どういった関数/導関数(微分)のグラフになるかをシミュレーターがすぐにアニメーション化してくれます!
微分シミュレーター:三角関数
このシミュレーターでは三角関数sin,cosを、その導関数(微分)と同時に描画します。その関係性を理解しましょう!
sinの微分
まずはsinからです。
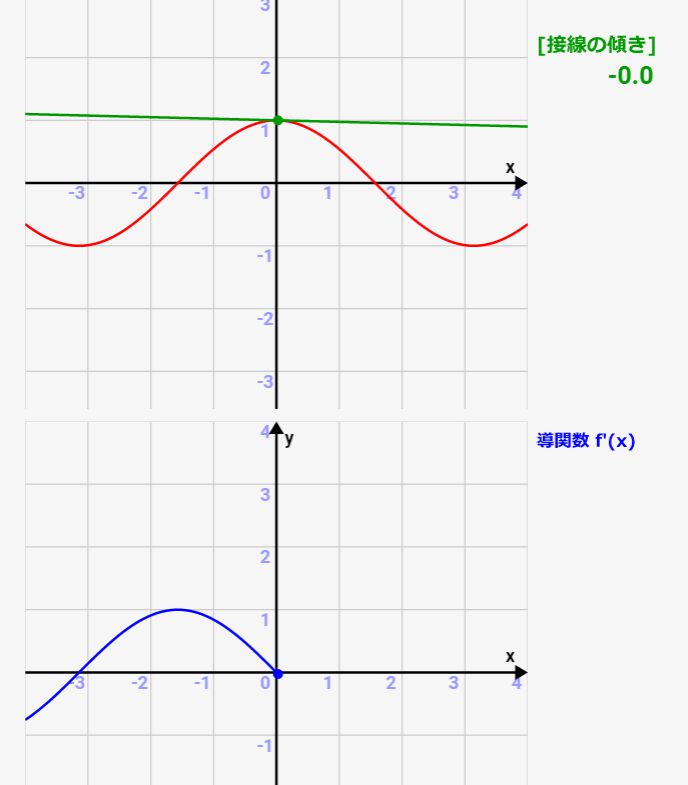
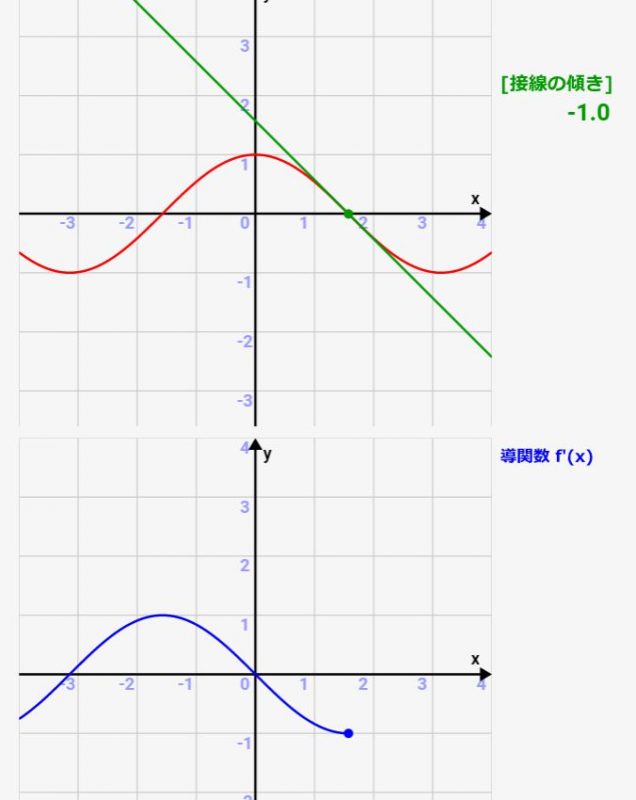
関数グラフがそれに従って描かれます。また、各点の接線とその傾きを調査しながら、導関数(微分)グラフを描いていきます!
sinの導関数は、\(y=cos(x)\)になります。この関係性をアニメーションで確認しましょう!
\( y= sin(x) \)
\( y= cos(x) \)
↓値を変えると、自動的にアニメーションが始まります!
cosの微分
次にcosの微分です。
関数グラフがそれに従って描かれます。また、各点の接線とその傾きを調査しながら、導関数(微分)グラフを描いていきます!
cosの導関数は、\(y= – sin(x)\)になります。この関係性をアニメーションで確認しましょう!
\( y= cos(x) \)
\( y= – sin(x) \)
↓値を変えると、自動的にアニメーションが始まります!
三角関数の導関数(微分)の要点
三角関数の導関数(微分)は上記の通り、
\( y= sin(x) ⇒ y’=cos(x)\)
[cos関数]
\( y= cos(x) ⇒ y’=-sin(x)\)
という関係になります。つまり、cosとsinは微分すると逆になるわけです(マイナス記号が付くかの違いありますが)。
というのも、sin/cosの差異は位相が違うのみで、形状は全く同じになるからです。
sin,cosでは関数/導関数が真逆の関係性になる!
sin,cosは、y= 1 or -1で極大/極小地点で平坦になり、そのとき導関数は0になります(微分の定義から当たり前ですが)
そして、関数がy=0を通る時、その接線の傾きがちょうど1 or -1となるため、導関数はy= 1 or -1となり極大/極小値になります。
つまり、「関数が極大/極小なら、導関数はy=0地点」「関数がy=0なら、導関数は極大/極小地点」という状況です。ですので、関数/導関数が真逆の関係性にあるわけです!
cosとsinが微分すると入れ替わるんですね!
- sin/cosを微分すると相互に入れ替わる
- sinθを微分すると cosθ になる
- cosθを微分すると – sinθ となる
↓本記事のような微分シミュレーターを各関数で用意しています。色んな関数で実際の「関数」と「導関数(微分)」の関係を確認してみて下さい!
↓cos,sinに関する他のシミュレーターの一覧はコチラ!
⇒「微分シミュレーター」カテゴリ記事一覧
その他関連カテゴリ