微分の意義を、物理の「位置 – 速度 – 加速度」シミュレーターで理解しよう![数学・物理入門]
数学の前回の記事までで、積分の基本的な考え方について説明しました。ただ、いまいち何のために積分をするのかが分かりにくいかと思います!
前回の記事では速度関数から位置関数を、積分を使って求める過程をシミュレーターで解説しました。今回はその逆で、「位置関数f(x)」から「速度関数f'(x)」「加速度関数f”(x)」を求める演算について、シミュレーターで解説します!
![微分の意義を、物理の「位置 – 速度 – 加速度」シミュレーターで理解しよう![数学・物理入門]](https://retu27.com/wp-content/uploads/rapture_20210425151353-475x500.jpg)
目次
「位置 – 速度 – 加速度」は微分・積分の関係にある!
これは前回記事の通りです。一般的に速度・加速度の定義は↓の通りです。
\( \displaystyle 速度(m/s) = \frac{距離(m)}{時間(s)} \)
\( \displaystyle 加速度(m/s^2) = \frac{速度(m/s)}{時間(s)} \)
ですが、これを微小量の細かい単位まで区切って定義すると↓のようになります。
位置関数をf(t)として
\( t時点での速度f'(t) \displaystyle = \lim_{ ⊿t \to 0 } \frac{f(t+⊿t) – f(t)}{⊿t} \)
\( t時点での加速度f”(t) \displaystyle = \lim_{ ⊿t \to 0 } \frac{f'(t+⊿t) – f'(t)}{⊿t} \)
これって、速度については導関数(微分)の定義そのものです。つまり、速度は位置関数f(t)の微分f'(t)と表すことが出来るのです!
↓導関数の定義。上記の速度の定義と全く同じ
$$ \large{ f'(x) = \displaystyle \lim_{ h \to 0 } \frac{f(x+h) – f(x)}{h} }$$
さらに、加速度についても同じような形になっており、「速度関数f'(t)の導関数(微分)」であることがわかります。つまり、加速度は位置関数の導関数の導関数なんです!このようなものを二階微分と呼びます。その名の通り、二階微分はベースの関数である位置関数を2回微分すれば求められるんです!
絵にすると↓のようなイメージになります。位置関数を一回微分すると速度関数になり、もう一回微分すると加速度関数になります!

前回記事の「速度→位置」の積分と違い、微分では不足情報はありません。なので、位置関数f(t)さえわかれば、速度と加速度関数を求めることができます!
「位置 – 速度 – 加速度」シミュレーター!定積分のイメージを理解しよう!
上記で説明した「位置 – 速度 – 加速度」の関係をシミュレーターを用いて確かめてみましょう!このシミュレーターではt=0~10の間で積分を行い、その間の位置/速度/加速度の変化をグラフで表示します。
の各パラメタa~dを↓のスライドバーで変更すると、それに合わせて速度関数f'(t)、加速度関数f”(t)が計算されます。
色んな値にパラメタを変化させて、どのような動きをするか確認してみましょう!
* チェックボックスで接線表示をON/OFFできます
\( {f(t)=} \) + 1\( {t^3 } \) + 1\( {t^2 } \) + 1\( {t } \) + 1
\( {f'(t)=} \) + 1\( {t^2 } \) + 1\( {t } \) + 1
\( {f”(t)=} \) + 1\( {t } \) + 1
↓値を変えると、自動的にアニメーションが始まります!
↑動的に再生速度を変えられます。左端で0にすると、一時停止となります。
シミュレーター結果の要点
要点1:位置関数が二次関数だと、等加速度運動になる
シミュレーターでa≠0の場合は3次関数になり、複雑な動きをします。しかし、a=0の場合は二次関数となり、こちらで解説している等加速度運動になります。この場合は↓の絵のように加速度が一定となり、速度は直線的に伸びていきます。これは2回微分すると、加速度が定数になるからです。

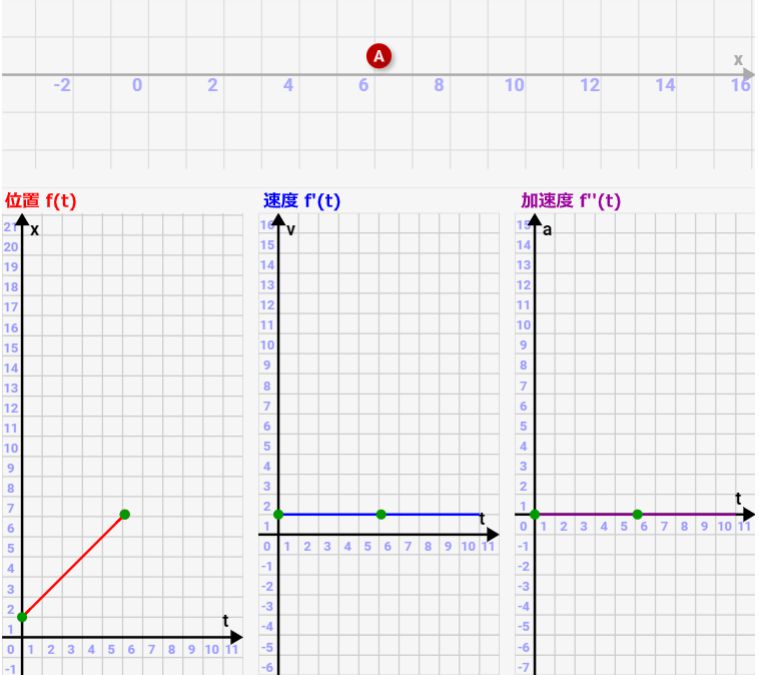
要点2:位置関数f(t)が一次関数だと、加速度は0になり、等速運動になる
シミュレーターでa=0,b=0にすると、位置関数f(t)は一次関数となります。この場合は等速運動になり、加速度は0になります。一次関数を微分すると定数になり、もう一回微分すると0になるからです。
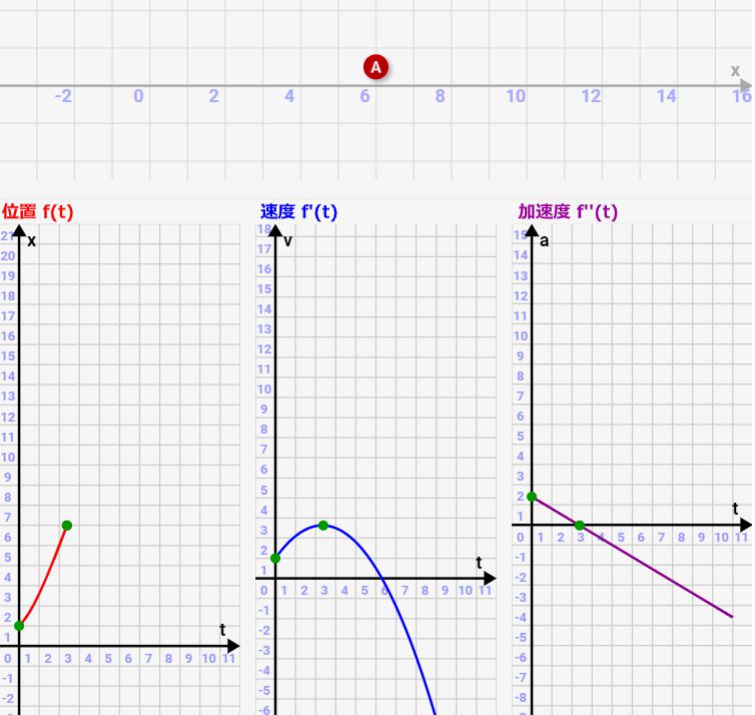
要点3:速度は加速度が0となるところで極小・極大となり、位置は速度が0となるとこで極小・極大となる
これも観察すれば分かります。速度が極小・極大となる点では、↓のように加速度が0になっています。
同様に、位置が極小・極大となる点では、速度が0になっています。
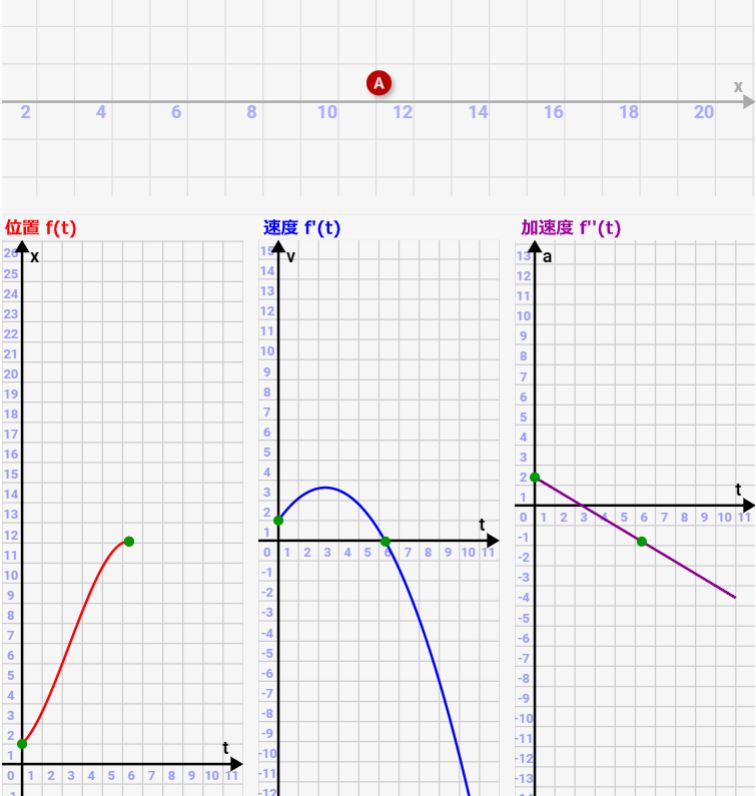
これは「関数f(x)が極小・極大になる点=導関数f'(x)=0の地点」という性質から自然とでてくる性質です!
まとめ:位置/速度/加速度の関係は微分を使うと、明らかになる!
最後にまとめです。物理学では等速運動や等加速度運動で、様々な公式があります。
そのような公式を覚えてもいいのですが、、、実はそれぞれが↓の絵のように微分・積分の関係にあるので、微分・積分をすればすぐに公式がでてきたりするんです。

この「位置 – 速度 – 加速度」の関係の例を知っておくと、数学の微積の理解も深まると思います!なので上記シミュレーターで理解を深めてください!
- 加速度は位置を2階微分したもの
- 位置関数が二次関数なら等加速度運動、一次関数なら等速度運動となる
⇒「微分の基礎」カテゴリ記事一覧
⇒「速度・加速度」カテゴリ記事一覧
その他関連カテゴリ