「指数関数」をシミュレーション/図解で理解![数学入門]
このページでは指数関数について解説していきます。「指数」の考え方については、前回記事で詳しくアニメーション等を用いて解説していますので、ソチラをご参照下さいませm(_ _)m
![「指数関数」をシミュレーション/図解で理解![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200412173831-497x500.jpg)
目次
おさらい:指数とは「同じ数を何回かけるか」を表したものです!
前回記事でも詳しく説明しましたが、簡単に例を用いておさらいしておきます。2を底とした場合、指数表記が↓のように出来ます。つまり、指数とは「同じ数を何回かけるか」を示したものです。
\( \normalsize{ 2^2 = 2 × 2 = 4 }\)
\( \normalsize{ 2^3 = 2 × 2 × 2 = 8 }\)
\( \normalsize{ 2^4 = 2 × 2 × 2 × 2 = 16 }\)
この考え方を拡張して指数が0やマイナスの時も以下のように計算できます。指数が0の時は値は1になり、指数がマイナスの時には逆数になります。
\( \large{ 2^{-1} = \frac{1}{2} }\)
\( \large{ 2^{-2} = \frac{1}{2 × 2} = \frac{1}{4} }\)
\( \large{ 2^{-3} = \frac{1}{2 × 2 × 2} = \frac{1}{8} }\)
このような考えをした時に、aを底とした指数関数を
$$ \large{y = a^x }$$
と定義できます。今回はこのグラフの性質について、シミュレーターを用いて解説していきます!底aはプラスという前提になります。
指数関数シミュレーターで実際のグラフを確認!
↓のスライドバーを動かすと、底aの値を変更できます!グラフがどのように変わるか確認してみましょう!
y = 2\( \normalsize{^x }\)
指数関数\( y=a^x \)の要点
要点1:通常はa>0の正数の場合のみを考える
通常指数関数を考えるときは、底aが正の数であること前提です。なぜなら、aが負の数、例えばa=-2だと、\((-2)^2=4,(-2)^{3}=-8\)と指数によってプラスになったり、マイナスになったりして扱いにくいからです。底が正の数なら値も常に正の数で扱いやすくなります。
これは、次の記事で解説する「対数関数」を扱うための前提でもあります!
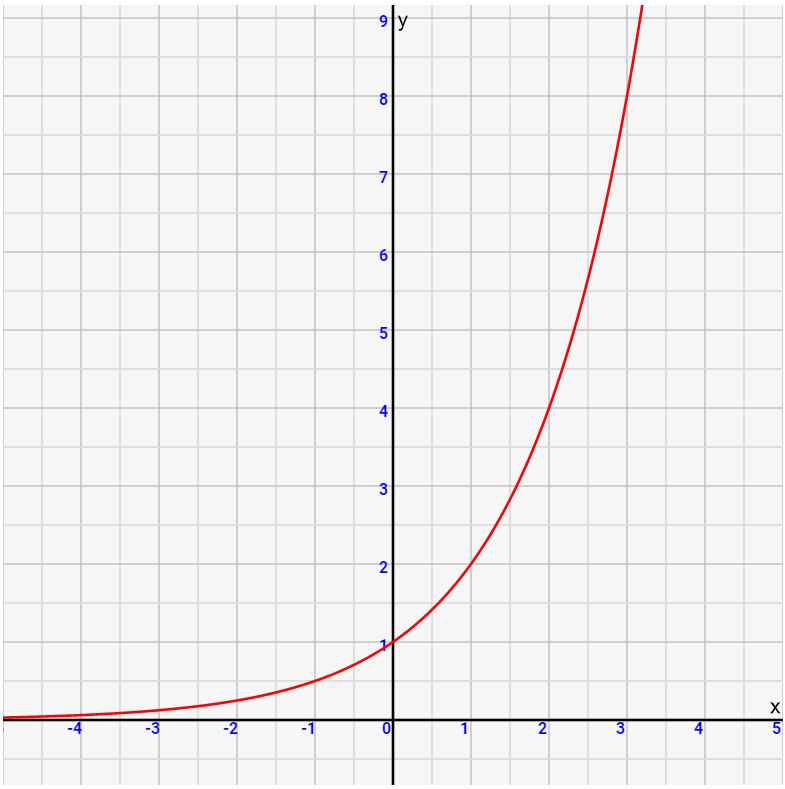
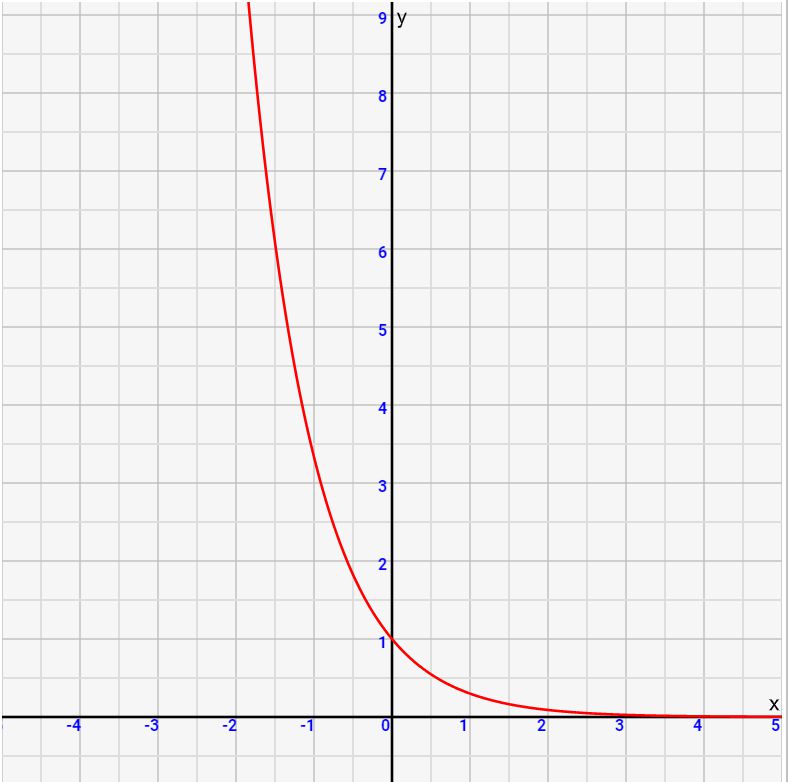
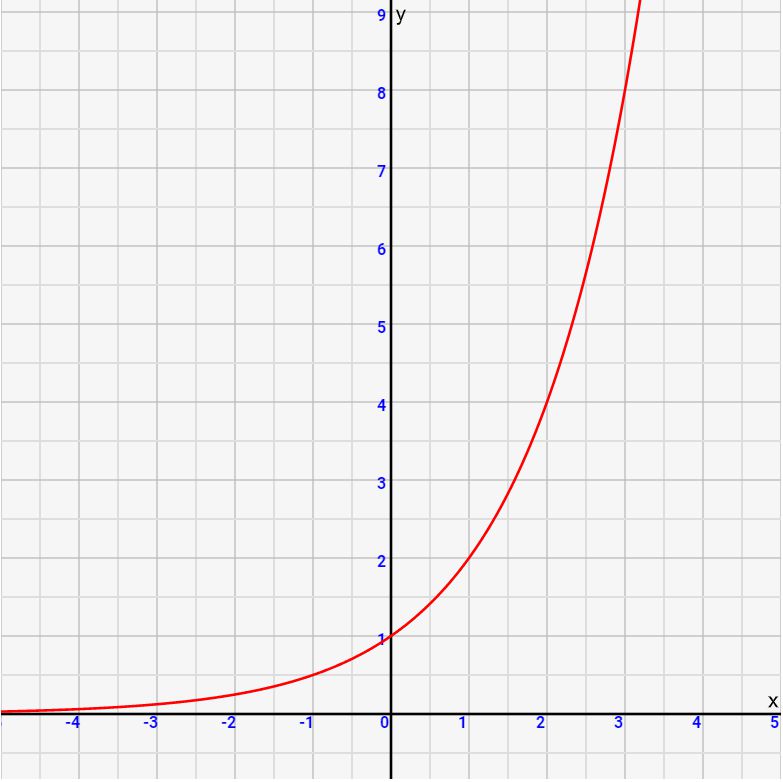
要点2:aが1以上なら単調増加、aが1以下なら単調減少となる
グラフから一目瞭然です。aがプラスならば、かける数が多くなるほど値が大きくなっていきますし、aががマイナスならば、かかけるほど数は低くなっていくためです。
要点3:aが1以外の時、yは0~+∞までの値をとる
aが1以上の時とaが1以下の時で、向きは違いますが、yの値は0以上+∞までの値をとります。これは、任意の正数は\( a^x \)の表記で表すことが出来る、ということを意味しています。
要点4:aが1の場合は1固定となる(直線)
1は何回かけても、何回割っても1です。なので↓のようなただの直線になります。
要点5:aが逆数になると、y軸対象なグラフとなる
例としてa=2とa=0.5(1/2)のグラフを見てみます。
y軸を中心として、両方のグラフが線対称になってますよね。これは2と0.5(1/2)が逆数となっているためです。指数関数は、前回記事解説の通り、以下の式がなりたちます。
$$ \large{ a^{-x} = \frac{1}{a^x} = {(\frac{1}{a})}^x }$$
つまり、xがマイナスのときはaの逆数の指数倍になるんです。a=2のときと、a=1/2のときでy軸中心に対称の関係になるんです!
次回予告:指数関数の考え方を拡張し、対数関数(log)を考えていきます!
上記のように、指数関数が単調増加/単調減少する形をとります。aが1以上か1以下で形が大きく変わること、逆数であれば対称関係になることが重大なポイントです!
次回はこの指数の考えを拡張した「対数関数(log)」について1から解説していこうと思います!
- 指数関数グラフはa>1なら右上がり、a<1なら右下がりのグラフになる
- 逆数同士は左右対称の指数関数グラフになる
⇒「指数関数」カテゴリ記事一覧
その他関連カテゴリ