関数とは何か？シミュレーションで分かりやすく理解！[数学入門]
2020-03-22 
関数とは何か
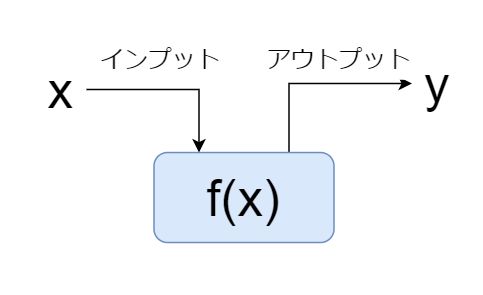
数学の分野、その他の学問でも非常に重要な考え方に「関数」というものがあります。関数とは「ある値を入れたら、何らかの計算がなされて、別の値が返ってくるもの」です。関数を数式で表すと以下のようになります。
$$ \large{y = f(x) }$$
これは「ある値xをインプットとして、関数f(x)に入れるとyという値がアウトプットとして返ってくる」ことを表しています。xがインプットで、yがアウトプットです。そして、その中間でf(x)という関数が何らかの計算をするわけですね。
↓イメージにするとこんな感じです。
この関数の具体例にはy=ax + bというようなものがあります。これは入力xにaをかけて、bを足したものがyにするという関数です。この関数をグラフ化すると、↓のようになります。xが決まれば、yの値も決まるので下図のようにグラフ化できるわけです。関数はこのように、入力xと出力yの関係性を示すものとなります。
関数の動きをシミュレーションで理解しよう！
それでは、この関数というものを実際にシミュレーションで実行して理解してみましょう！↓のシミュレーターでは
$$ \large{y = x^2 – 4 }$$
というものを例題としています。この関数で、実際にインプットxからアウトプットyにどのように計算されていっているのかをアニメーション化してみました。「実行！」ボタンを押すたびに、各x点でyの計算がされて、グラフが図示されていきます！何回か実行ボタンを押して、この関係を理解していきましょう！
このように、各x点でf(x)に値を入れて、yを計算すれば関数グラフが作成できます！
主な関数の種類
関数には、上記のようなもの以外にも多くの種類があります。この一部が以下のようなものです。これらは高校までの数学で非常に重要なものになってきます。
1次関数：\( \large{y = ax + b }\)
2次関数：\( \large{y = ax^2 +bx +c }\)
指数関数：\( \large{y = a^x }\)
対数関数：\( \large{y = log(x) }\)
三角関数：\( \large{y = sin(x) }\)
本サイトではこれらの関数を、実際に値を変えてシミュレーションできる形で分かりやすく説明していく予定です！
- 関数はxをインプットとして、yを出力する
- どのようにxからyを計算するかは関数の定義による
⇒「関数」カテゴリ記事一覧
その他関連カテゴリ