対数関数(log)をシミュレーション/図解で理解![数学入門]
目次
対数とは何か?
前回の記事では、指数関数について細かく解説しました。本記事では、それに関連した対数関数について解説します。
対数とは「ある数aを何乗すればxになるか示した数」のことです。a=2で、x=8なら\(2^3=8\)で対数は3と言えます。このような対数を求める関数を対数関数といい、\(y=log_{a} x\)という形で表します。底aはlogの後に小さく下に書いて示します。この中でaは累乗する数(底)であり、xは累乗したあとに求められる数です。
つまり、
$$ \large{ a^y = x ⇔ y = log_{a} x
}$$
という関係になります。aをy乗したときxになる。そのようなyを、aとxから求めるのが対数関数(log)になります。
対数関数(log)シミュレーターで対数関数のイメージを理解しよう!
対数関数は上で述べたような定義になります。ただ、このままだとわかりにくいので実際のグラフを見てイメージを掴みましょう!
↓のシミュレーターでは底aの数を自由に変えられますので、aを変更して対数関数(log)のグラフ形状がどのように変化するのか確認してみてください!
\( {y = \log_{ a } x } \)
対数関数の要点
底aは正の数であることは基本前提
上記の関数では、底aが正である事が前提です。これは指数関数での前提と同じですね。底が負の数だと、値が発散するので基本は考えません。
定義範囲はx>0
対数関数の定義範囲は、x>0のみで定義されます。底aが正である限り、絶対に累乗した値も正の数となるので。
底aが1の場合は考えない
底aが1の場合、何度1をかけても1のままです。ですので、\(log_1 x \)に解はなく、定義できません。
x=1の場合は必ずy=0となる
これは底aがどんな正の数であれ、\( a^0=1 ⇒ log_{a} 1 = 0 \)となるからです。
yの範囲は-∞~+∞まで全域で、単調増加 or 単調減少
これが重要なポイントです。aが1以外の値の場合、下図のように対数関数は単調増加 or 単調減少になります。
a<1のときは下図のように+∞~-∞への単調減少関数になります

ここが重要なポイントなのですが、対数関数はyの値を決めると、必ず一意のxを決められます。対応するxが存在しないこともないし、2つ以上対応するxが存在することもないです。また、逆も同じでxの値を決めると、必ず一意のyが決められます。
ですので、
$$ \large{ x = y ⇔ log_{a} x = log_{a} y
}$$
という式変形が成立します。底aがどんな正の数であれ成り立ちます(a=1除く)。当たり前のようですが、とても意味あるものです。どんな等号式であれ、logを付けたり外したりして考えることが可能になるわけです!
重要ポイント!指数関数と対数関数は逆関数!xy軸反転すれば描けます!
ここで重要なのが、指数関数と対数関数は逆関数の関係にあるということです。逆関数とは、ある関数のxとyをひっくり返した時に対応する関数同士のことですね。つまり、
$$ \large{ y=a^x }$$
という指数関数のxとyを逆転させると、
$$ \large{ x=a^y ⇒ y=log_{a} x }$$
対数関数になります。逆関数とは、関数グラフのxとyを反転させたグラフになります。
ですので、 \(y=2^x\)のグラフ図に対し、
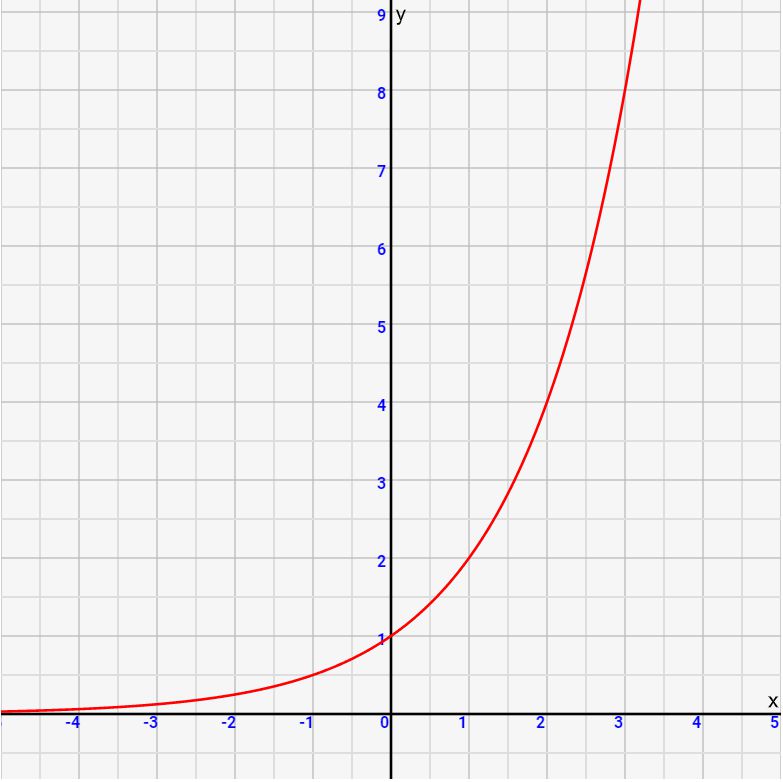
この逆関数\(y=log_{2} x \)のグラフは上の図をxy反転させたグラフ
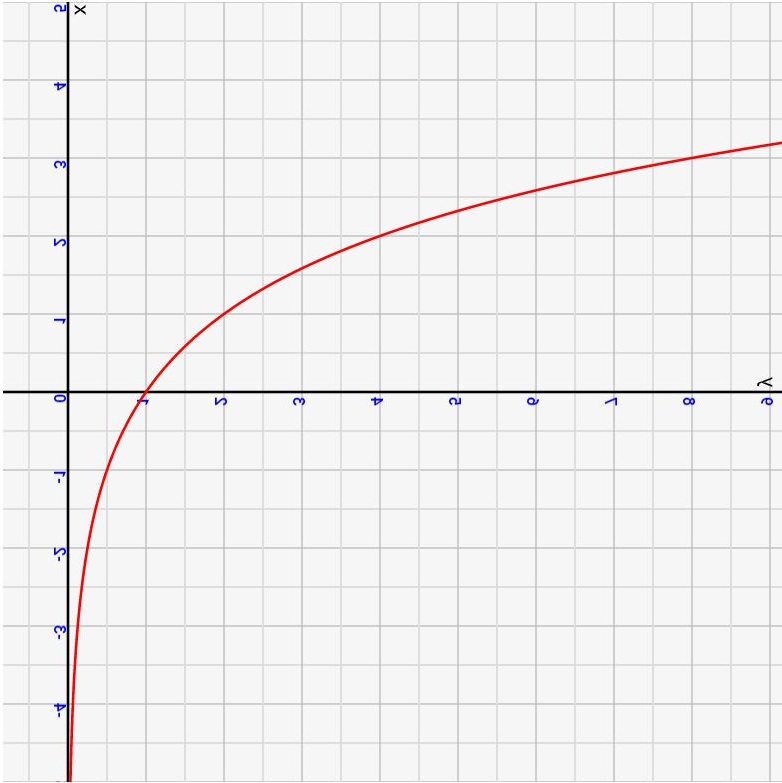
になります。言い換えると、指数関数上のyを指定したときに、それに対応したxを求めるのが対数関数(log)になります。こう考えると簡単ですね!
指数関数と対数関数の逆関数関係をシミュレーターで体感しよう!
上で述べた定義をまとめると、対数関数(log)は「aを何乗すればyになるかを求める関数」です。また、上で述べた通り、対数関数は指数関数の逆関数です。ですので、再度になりますが、指数関数でyを指定したときに、対応するxを求めるのが対数関数(log)なんです!
実際にこの指数関数と対数関数値の逆関数の関係をシミュレーターで確認してみましょう!
例としてわかりやすい底a=2の場合でシミュレーションしてみます。↓のグラフの赤線は指数関数 \( {y = 2^x } \)の関数グラフです。下のスライダーで対数関数の入力xを指定できますが、逆関数の指数関数上ではyの値を指定したことになります(グラフ上の青い横線がこのy値です)。
指数関数がこのyの値となるときのx(青い線と赤い線が交わる点)こそ、対数関数で求めたい値yになります!
\( {y = \log_{ 2 } x } \) = 2
↓指数関数上の対応するxが、対数関数の値y↑と一致している事を確認してみてください!
次回は対数関数(log)の公式について考えていきます!
ここまで述べた通り、対数関数(log)は指数関数の逆関数であり、指数関数に戻して考えるとイメージがつきやすいです!上記のシミュレーションのイメージを頭に入れて、理解していきましょう!
この対数関数(log)、いくつかの式変形の公式があります。次回のその変形について、シミュレーターを用いて解説していきます!
- aを何乗したらxになるかを求めるのが対数関数(log)
- 指数関数と対数関数は逆関数の関係にある!
⇒「数学」カテゴリ記事一覧
その他関連カテゴリ


















