一次関数/線形関数をシミュレーション図で理解！[数学入門]

2020-03-23　 関数

一次関数とはy=ax+bで表せる関数。グラフは必ず直線になります

このページでは簡単に数学の基本である一次関数を説明します。一次関数は線形関数とも呼ばれます。それは関数グラフが必ず直線になるからです。
　
一次関数は以下の式で表せます。見たとおり、入力xにaを乗算して、bを加算した関数になります。

この一次関数/線形関数は以下のようなグラフになります。xが1増える → yがaだけ増えるという比例関係にあり、直線的なグラフになります。

　

シミュレーターで自由に一次関数を操作して理解しよう！

上記のような\(\large{y = ax + b}\)という一次関数/線形関数を下記のシミュレーターで自由自在に操ってグラフ描画することが可能です！
　
↓ a,bの値を操作してみて、実際にどんなグラフになるか実験/確認してみましょう！リアルタイムに関数が変わり、グラフ形状も変わっていきます！

一次関数の要点

要点1：aを傾き、bを切片と呼ぶ。y軸上では必ずbを通る

上のシミュレーターで分かる通り、aを変化させると線の傾き(角度)が、bを操るとグラフが上下することが分かると思います。また、y軸上を見ると必ずy=bの点を通っていることが分かります。

このaを「傾き」、bを「切片」と呼びます。傾きとは「xが1変化したときに、yがいくつ変化するか」の値です。切片とは、「関数グラフとy軸の交点」のことです。上記の通り、一次関数/線形関数では必ず(x,y)=(0,b)を通り、bが切片になります！

要点2：a＞0で単調増加、a＜0で単調減少グラフとなる

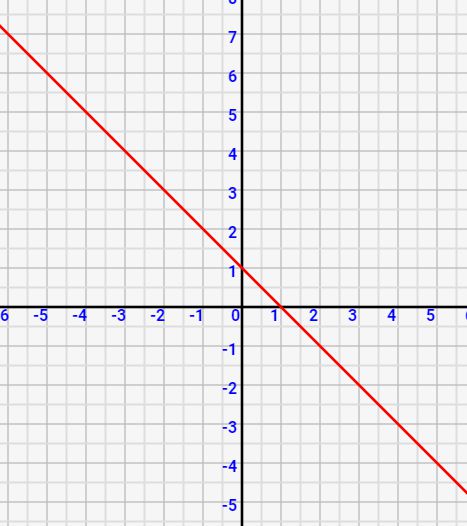
これは要点1からも言えることですね。aは傾きであり、aがプラスであればxが増えるたびにyも増加していきます。

逆に、aがマイナスであれば、xが増えるたびにyは減少していきます。単調減少ですね。

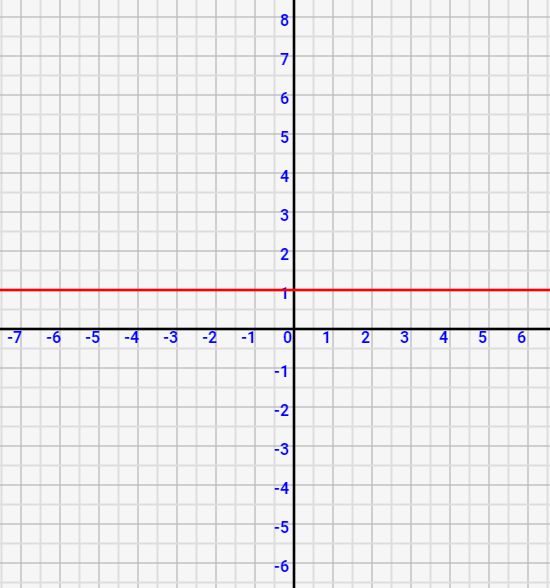
特殊なのはa=0の場合です。この場合y=bとなり、yが固定値となります。つまり、↓のような横線になります。

　

まとめ

一次関数/線形関数は上記の通り、シンプルな関数です。しかし、汎用性の高い非常に重要な関数になります。是非上記のシミュレーションでグラフ形状のイメージを身に着けてください＞＜
　

[関連記事] 数学入門：関数

1．関数とは何か？

2．合成関数

3．関数の平行移動

4．一次関数/線形関数(本記事)

5．二次関数

6．三角関数(sin,cos)

7．指数関数

8．対数関数(log)

9．対数関数(log)の演算法則