二次関数をシミュレーション/図解で理解![数学入門]
前回、一次関数(y=ax+b)についてシミュレータを用いて説明をしました。今回は二次関数の説明です。シミュレーターでその概要を理解しましょう!
![二次関数をシミュレーション/図解で理解![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200323210945-441x500.jpg)
目次
二次関数はU字型の曲線グラフになります
二次関数は以下のような形で表せる関数です。
$$ \large{y = ax^2 + bx + c }$$
一次関数との違いは「ax^2」という項が入ることです。グラフはa=0出ない限り、下図のような曲線になります。というより、a=0の場合は一次関数と同じですよね。
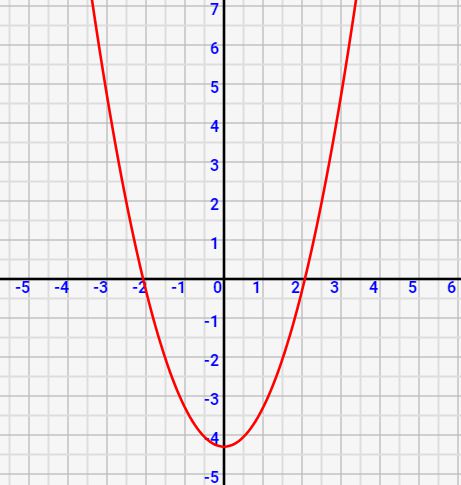
この二次関数グラフ、実際に手を動かしてどんな形状になるのかシミュレータで確認してみましょう!
シミュレーターで自由に二次関数を操作して理解しよう!
上記のような\(\large{y = ax^2 + bx + c}\)という二次関数を下記のシミュレーターで自由自在に操ってグラフ描画することが可能です!
\( {y=} \) + 1\( {x^2 } \) + 1\( {x } \) + 1
二次関数の要点
要点1:aによってU字の形状が決まる。
aを変化させると、U字の形状が変わります。aの絶対値が大きいほど、傾斜の強いU字型になります。逆にいうと、aが一定ならば、b,cが変わってきてもその形状は同一になります。
要点2:cによってU字の上下の位置がきまる
cは切片になります。切片は、「関数グラフとy軸の交点」のことです。x=0であれば、y=cとなるため、y軸上では必ずc点を通ることになります。関数移動の観点からも分かる通り、このcによって、U字グラフの上下の位置が決まります。
要点3:bによってU字の位置が変わる。でもその変わり方は複雑…
上記のa,cに対する変化はわかりやすいものでした。しかし、bの変動はやや複雑です。bが変動すると、U字グラフの位置が変わりますが、単純な上下動や左右動でなく、複雑な動きをします。
⇒ 式変換をして、わかりやすい形に変換してあげることが望ましいです(詳細は別記事で開設予定)
要点4:a>0でU字グラフ、a<0で逆U字グラフとなる
二次関数のグラフはU字型になりますが、aの符号によってその向きが変わります。
[a>0の場合:U字型]
このときのU字の先端を極小点といいます。

[a<0の場合:逆U字型]
このときの逆U字の先端を極大点といいます。
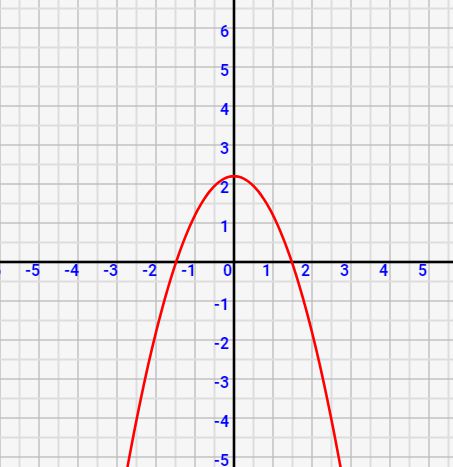
a=0の場合は上記の通り、一次関数となり形状は直線になります。
まとめ
二次関数は、U字型のグラフになります。その形状は\(x^2\)の係数であるaによって変わり、xの係数であるbや切片cによってそのU字の極小点/極大点が移動します。また、cは一次関数と同じく、切片(y軸との交点)を決める要素になります。
- 二次関数は放物線を描く
- aがプラスかマイナスかで、どちら向きの放物線になるかが決まる
⇒「二次関数」カテゴリ記事一覧
その他関連カテゴリ



















