「点電荷のエネルギー」をシミュレーションで理解しよう![物理入門]
前回の記事で、複数の電荷がある場合のクーロン力について解説しました。今回は点電荷がなすエネルギーについて考察していきます!
![「点電荷のエネルギー」をシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/20211027006974-500x361.png)
目次
クーロン力のおさらい
最初に前回までの記事のおさらいです。2つの電荷にかかるクーロン力は↓のように計算できます。
\( \displaystyle \large{F = k \frac{|q_1||q_2|}{r^{2}}} \)
- \(q_1\),\(q_2\) : 電荷1,2の電気量[C]
- \(r\) : 2電荷間の距離[m]
- \(k\) : 比例係数で、真空中で\(9.0 × 10^9\)
2電荷が同じ符号の時:離す方向
2電荷が違う符号の時:引き合う方向
大事なポイントは「2つの電荷は近づくほど強くなる」「電荷の符号が同じか否かで方向が変わる」です。↑のように、電荷の符号のパターンでかかる力の方向が変わるんですね。
点電荷がなすエネルギーを考えてみる
こちらのページで解説している通り、仕事Wはかかる力を距離xで積分することで計算できます。
点電荷Qが点電荷qに対してかける力Fは公式の通り、↓で定義できます。これをx(この式では距離r)で積分すれば、↓点電荷がなす仕事が計算できるわけです!
\( \displaystyle \large{ F = k \frac{Q q}{r^{2}} } \)
- \(Q\),\(q\) : 各電荷の電気量[C]
- \(r\) : 2電荷間の距離[m]
- \(k\) : 比例係数で、真空中で\(9.0 × 10^9\)
数学のページで解説している公式で積分すると、、、↓のようになります。
\( \displaystyle 積分関数W(r) = – k \frac{Q q}{r} \)
距離\(r_1\)から\(r_2\)まで移動させる時の仕事Wは、↑の関数に対して定積分のように差分をとることで計算可能です。
\( \displaystyle W = W(r_2) – W(r_1) = – k \frac{Q q}{r_2} + k \frac{Q q}{r_1} \)
ここで、無限に離れた距離r=∞では、W(∞)=0となるので、\(r_2=∞\)を基準点と考えることにすると、、、
\( \displaystyle W = k \frac{Q q}{r_1} \)
とできます。つまり、\(r_1\)から∞にいくまでに、点電荷qには↑の仕事を加えられるわけです。これこそが、点電荷がなすエネルギーUなのです!
\( \displaystyle U = k \frac{Q q}{r} \)
- \(Q\),\(q\) : 各電荷の電気量[C]
- \(r\) : 2電荷間の距離[m]
- \(k\) : 比例係数で、真空中で\(9.0 × 10^9\)
点電荷は互いの距離を短くなるほどエネルギーが増大していきます。ただし、2つの符号が異なる場合はマイナスエネルギーが拡大していきます。
電場・電界をシミュレーターで確認しよう!
上記で考察した「点電荷のエネルギー」を考察してみましょう!
- スライドバーによって電荷Q,電荷q,距離rが変えられます
- 電荷Qは位置x=0に固定で、電荷qはx=rの位置に配置されます
- 電荷は赤色でプラス、青色でマイナスを表します
- グラフは電荷Q,qによる各位置でのエネルギーを図示したものです
- 電荷の量を変えてみて、グラフがどう変わるか確認してみましょう
- 距離rを変化させ、エネルギーUがどのように変わるか確認しましょう
シミュレーター結果の要点
シミュレーターで電荷を変えてみると以下のことが分かります。
電荷が大きくなると、エネルギーが大きくなる
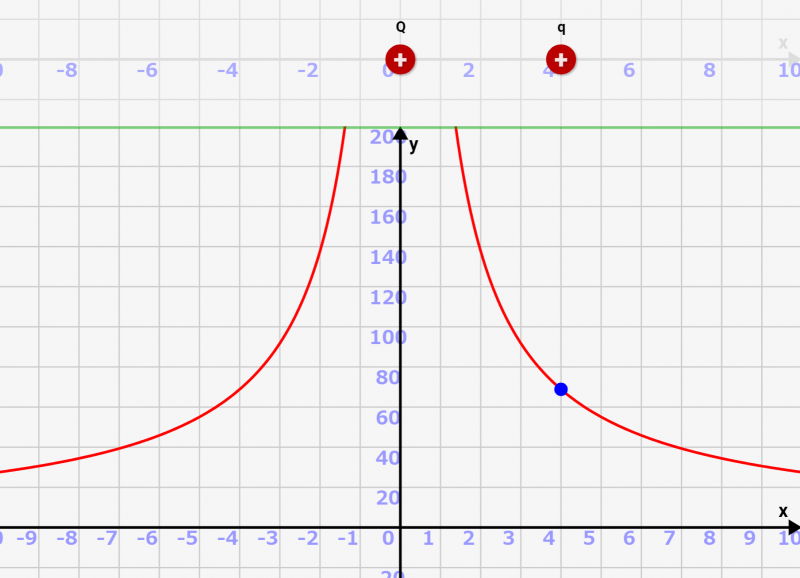
電荷Qと電荷qの位置が近いほど、エネルギーが高くなります
それだけ、力が加わるというわけですね!
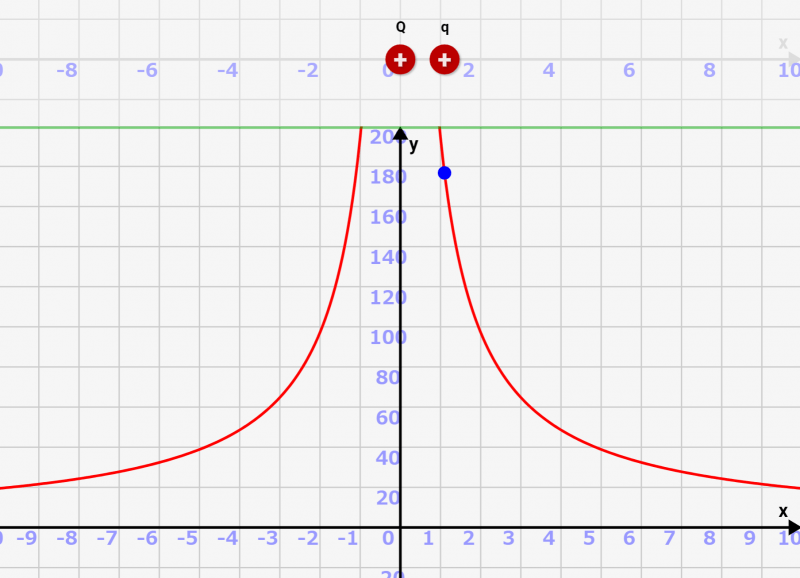
エネルギーが高い=高い位置に有り、他エネルギーに変えられる状態!
電荷Q,qを近い位置に持っていくと、エネルギーが上昇します。これは、位置エネルギーでいう「高い位置に物体を持っていく」ことと同じです。高い位置にもっていけば、それだけ他のエネルギーに変換できる能力を持つということなのです。

- クーロン力も力なので、位置エネルギーとみなせる
- 電荷が同じ符号なら、近いほどエネルギーが高くなる
- 異符号なら、逆に遠いところが一番高いエネルギーとみなせる
次回は、この点電荷でなく、面に一様に分散する電荷について考えてみます。
⇒「静電気・電場」カテゴリ記事一覧
その他関連カテゴリ
















