「電気回路: 並列の抵抗」をシミュレーションで理解しよう![物理入門]
前回記事で説明したオームの法則を用いて、様々な電気回路をシミュレート/解説していきます!
今回は「電気回路: 並列の抵抗」についてのシミュレーターです!
![「電気回路: 並列の抵抗」をシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/20211106007046-500x379.jpg)
目次
おさらい:オームの法則
電源は、電位を上げて、より電流を流れやすくするものです。電位・電圧が高いほど、位置が高くなり、抵抗があっても電流を速く流せるようになるイメージです。

電圧・電位Vと、流れる電流I・抵抗Rの間には↓のような関係があります。これがオームの法則です!
\( \displaystyle \large V = IR \)
- V : 電圧[V]
- I : 電流[A]
- R : 抵抗[\(Ω\)]
「並列の抵抗」での計算の仕方
「並列の抵抗」とは↓の回路図のように、回路が枝分かれして抵抗が横にならんだものです。
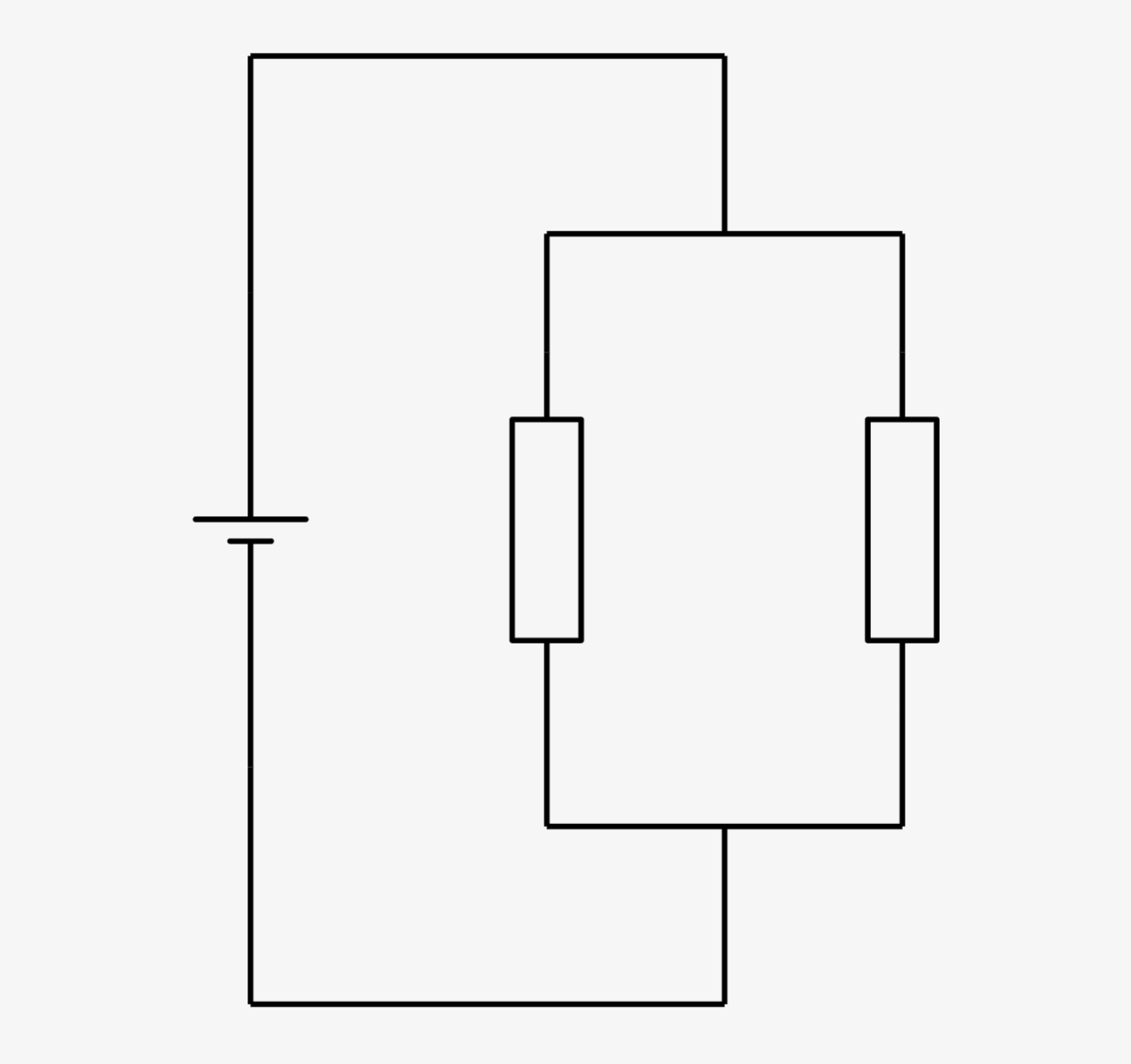
このように抵抗\(R_1\)と抵抗\(R_2\)の2つが並列であった場合、合成抵抗Rは↓のようになります。合成抵抗とは、2つの平行抵抗により実質的に一つの抵抗とみなした時の抵抗値です!
\( \displaystyle \large \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} \)
少しややこしい式なので、以下解説していきます。
並列な抵抗の電位差はすべて同じ
まず、↓のように並列の抵抗があった場合、この2つの抵抗で減少する電位は同じでなければいけません。(図中で紫点部分が抵抗を示しており、高さが各地点の電位を示しています)
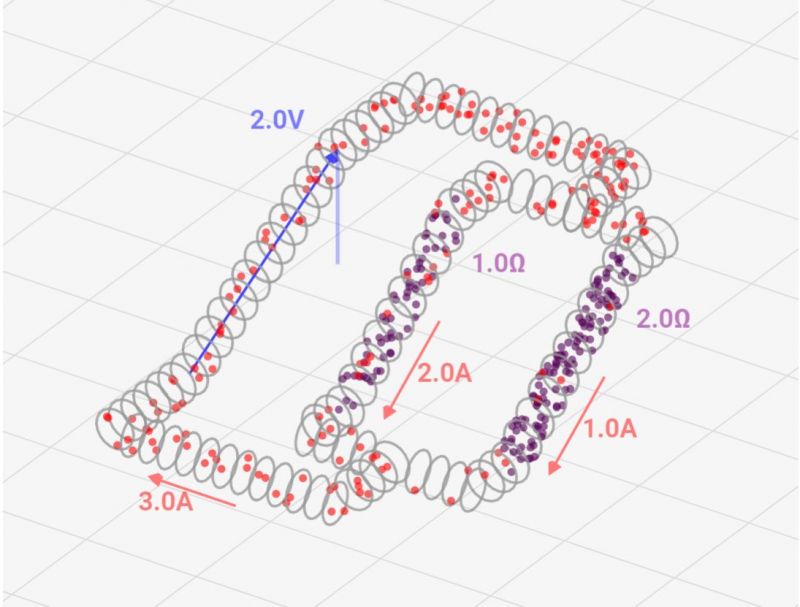
後日記事で説明しますが、ある地点の電位は必ず1つの値に収束するので、2つの地点に挟まれた抵抗\(R_1\)と抵抗\(R_2\)の電位は必ず同じにならないといけないのです。そのため「抵抗1の電圧\(V_1\)」と「抵抗2の電圧\(V_2\)」は↓のような関係式になります。
\( \displaystyle V_1 = V_2 \)
全ての抵抗に流れる電流を足すと、分岐前の電流量になる
電流は、川の水流みたいなものです。もし回路内で分岐したら、その流量は分散され、送料は分岐前と同じになるはずなんです。
そのため、回路全体に流れる電流をIとすると、「抵抗1に流れる電流\(I_1\)」と「抵抗2に流れる電流\(I_2\)」は以下の関係になります。
\( \displaystyle \large I = I_1 + I_2 \)
並列な箇所の電流全てたすと、総電流量Iに一致するわけです!
流れる電流は抵抗値の比率と逆になる
↑の2式を変形していくと、、↓のようになります。
↓ \(V_1 = I_1 R_1 \)と\(V_2 = I_2 R_2 \)代入
\( \displaystyle I_1 R_1= I_2 R_2\)
↓
\( \displaystyle I_1 = \frac{R_2}{R_1} I_2 \)
これは電流量が抵抗値の逆配分になることを意味します。例えば\(R_1=1,R_2=2\)なら、電流\(I_1\)は\(I_2\)の2倍になるわけです。
省略しますが、これを\( I = I_1 + I_2\)に代入すれば、↓のように逆数での関係が成り立つことを示せます!
\( \displaystyle \large \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} \)
また電流量\(I_1\),\(I_2\)は以下のように逆配分的になります。
[抵抗1に流れる電流]
\( \displaystyle \large I_1 = \frac{R_2}{R_1 + R_2} I \)
[抵抗2に流れる電流]
\( \displaystyle \large I_2 = \frac{R_1}{R_1 + R_2} I \)
「電気回路: 並列の抵抗」をシミュレーターで確認しよう!
それでは並列の抵抗による合成抵抗値の変化を、シミュレーターで確認してみましょう!
- 電源は青矢印で、抵抗は紫点部分で示しています
- 高さで各位置の電位の高さを表しています
- スライドバーによって2つの抵抗\(R_1,R_2\),電源電圧が変えられます
- ↑で計算したような、合成抵抗の式を満たすことを確認しましょう
- 抵抗1,2の逆比率で、各抵抗に電流が流れることを確認しましょう
- 各抵抗に流れる電流の合計が、総合電流と一致することを確認しましょう
シミュレーター結果の要点
↑で解説してきたように、並列の抵抗がある場合、抵抗の逆比率で電流が配分されます。↓は「抵抗1:抵抗2=1:4」で設定した図ですが、\(\frac{4}{5}\)は抵抗量の低い抵抗1に流れているのが分かると思います。図でも分かるように、障害物の少ない抵抗が低い経路に電流は寄るってことなんです!

また、分岐する場合は流れる電流/電荷が分配されるだけで、そこで急に電荷が増えたり減ったりするわけでないという考え方はすごく重要です!この辺りを次の記事で解説していきます!
- 電流経路が違っても、2つの経路の電圧は必ず同じになる
- 並行抵抗に対して、電流は抵抗値の逆の配分で流れていく(低い抵抗側に、電流は多く流れる)
⇒「電気回路・キルヒホッフの法則」カテゴリ記事一覧
その他関連カテゴリ














