「ガウスの法則」をシミュレーションで理解しよう![物理入門]
前回の記事で、電気力線について解説しました。今回はこの電気力線を3次元で考察して「ガウスの法則」を検証していきます!
目次
クーロン力のおさらい
クーロン力
最初に前回記事のおさらいです。2つの電荷にかかるクーロン力は↓のように計算できます。
![「ガウスの法則」をシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/rapture_20210408211359-500x479.jpg)
\( \displaystyle \large{F = k \frac{|q_1||q_2|}{r^{2}}} \)
- \(q_1\),\(q_2\) : 電荷1,2の電気量[C]
- \(r\) : 2電荷間の距離[m]
- \(k\) : 比例係数で、真空中で\(9.0 × 10^9\)
2電荷が同じ符号の時:離す方向
2電荷が違う符号の時:引き合う方向
大事なポイントは「2つの電荷は近づくほど強くなる」「電荷の符号が同じか否かで方向が変わる」です。↑のように、電荷の符号のパターンでかかる力の方向が変わるんですね。
電気力線
電気力線は、前回記事で作成したように「各点の合成電界を計算して描いた図」です。各点でどちらの向きに電界が向いているか示したものです。
↓のように「プラス電荷から出て、一本の線を描いて、マイナス電荷に収束していく」という動きになります。まるで線が電荷から出ているようです!

クーロン力を3次元で考えてみると、、、
3次元版の電気力線
今までは分かりやすいように2次元まででクーロン力を考えてきましたが、実際はクーロン力は3次元で発生します。
このときに、実は↑の電気力線と同じように「電荷から固定数の線が出てくる」という考え方ができます。そのイメージが↓になります。中心の電荷から線がでてくるイメージです。

距離r離れた球の表面積を考察してみる
ここで、電荷から半径rの球面の表面積を考えてみます。↑の図の緑の球面ですね。これは数学的な公式から↓のように求められます。
半径rの球の表面積 = \( \displaystyle \large{4πr^2}\)
ここで、3次元では各点で単位面積 \(1m^2\)あたり電界\(E=k \frac{q}{r^{2}}\)本だけ電気力線が通っていると考えいます(負電荷の場合はマイナスとしてカウントする)。そして、半径rでの球表面全体で何本の電気力線が通っているのか考えると、、、、
半径r球の力線総数 = \( \large E × 4πr^2 \)
= \(\large \displaystyle \frac{4πr^2 kq}{r^{2}} \) : \( \displaystyle \large 4πkq\)
- q : 電荷の電気量[C]
- k : 比例係数。真空中で\(9.0 × 10^9\)
となるんです。つまり、電気力線=\(4πkq\)となるため、半径rに依存しないのです!故に、距離によらず、電荷から出ている電気力線は一定と言えるといえます。
つまり、↓のイメージで正しいのです。電荷中心から特定本数の線がでていて、それは電荷のクーロン量で決まります。

「ガウスの法則」をシミュレーターで確認しよう!
それでは「ガウスの法則」を3次元のシミュレーションで実際に見て確認しましょう!
- スライドバーによって電荷,球の半径rが変えられます
- 分かりやすいように、電気力線本数=10*電荷となるように図示しています
- 電荷の量によって電気力線が比例して増えることを確認しましょう
- 球の半径が変わっても、貫く本数が変わらないことを確認しましょう
- 下の表示角度で見やすいように縦角度を変えられます
- 電荷の符号が逆になると、矢印が逆になることを確認しましょう
rでのクーロン力:
貫く電気力線: 本
* 「電気力線本数=クーロン力 × 球の表面積」という関係になっています
↓表示角度(上下)をコチラのバーで調整可能です!
シミュレーション結果の要点
電荷と力線本数が比例
シミュレーターで↓のように電荷の量に比例して、力線の本数が変わるのが観察できると思います。
[電荷=1.0Cの場合]
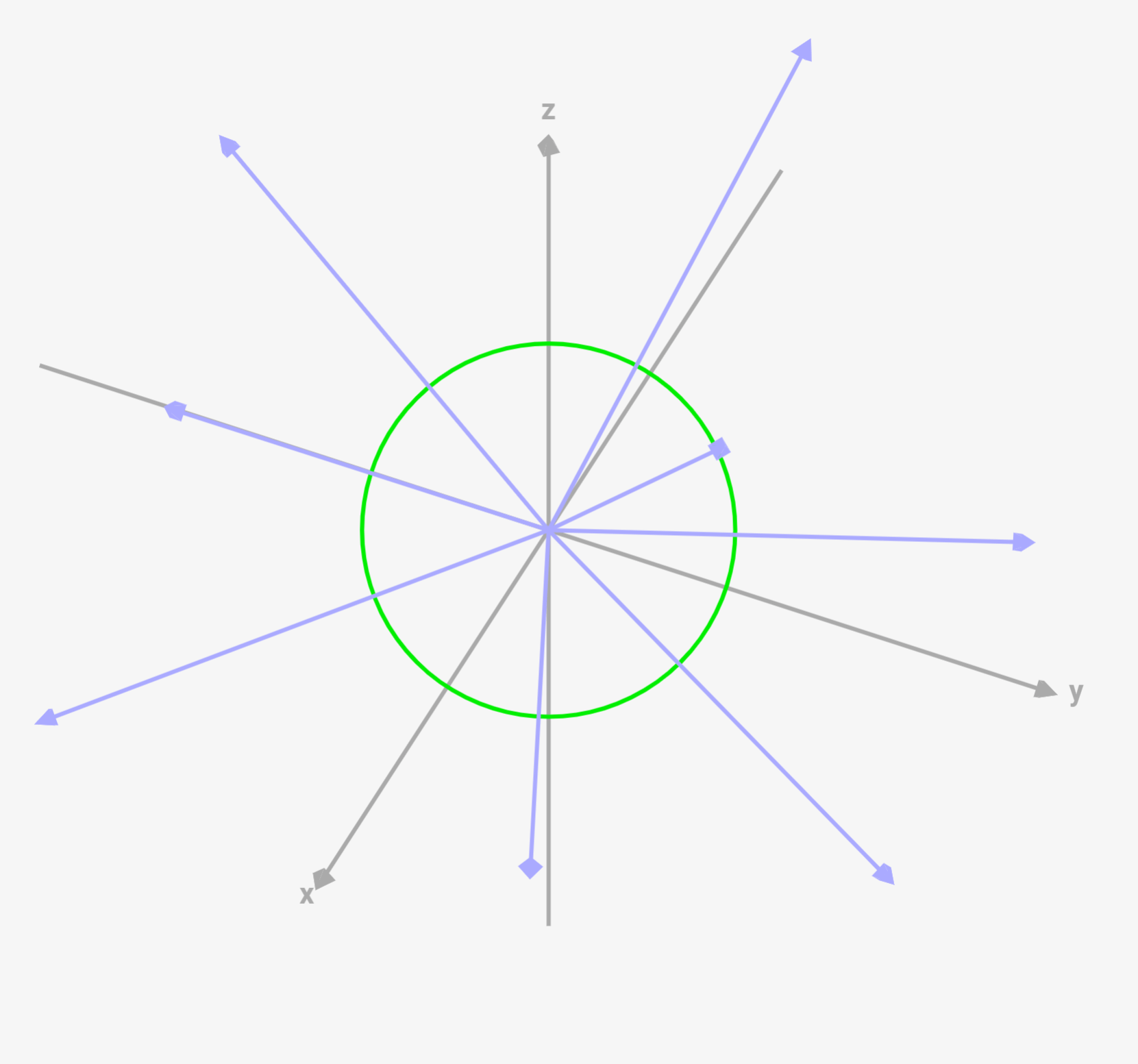
[電荷=10.0Cの場合]
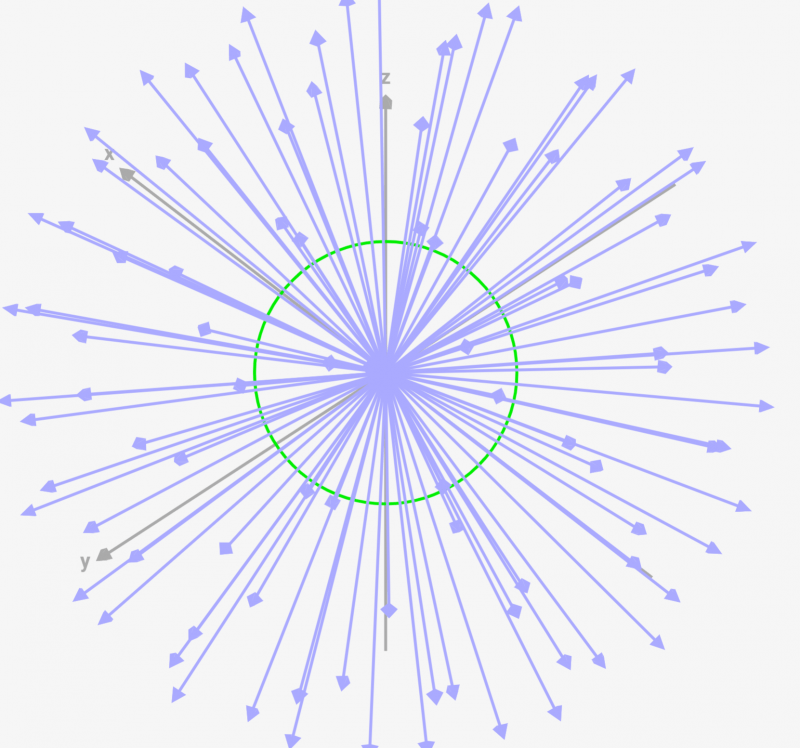
電荷がマイナスになると矢印が逆になる
これは二次元のときと同じですが、プラス電荷の場合は外側に出ていく方向になるのに対し、マイナス電荷の場合は矢印が入ってくる方向になり、逆向きになります。
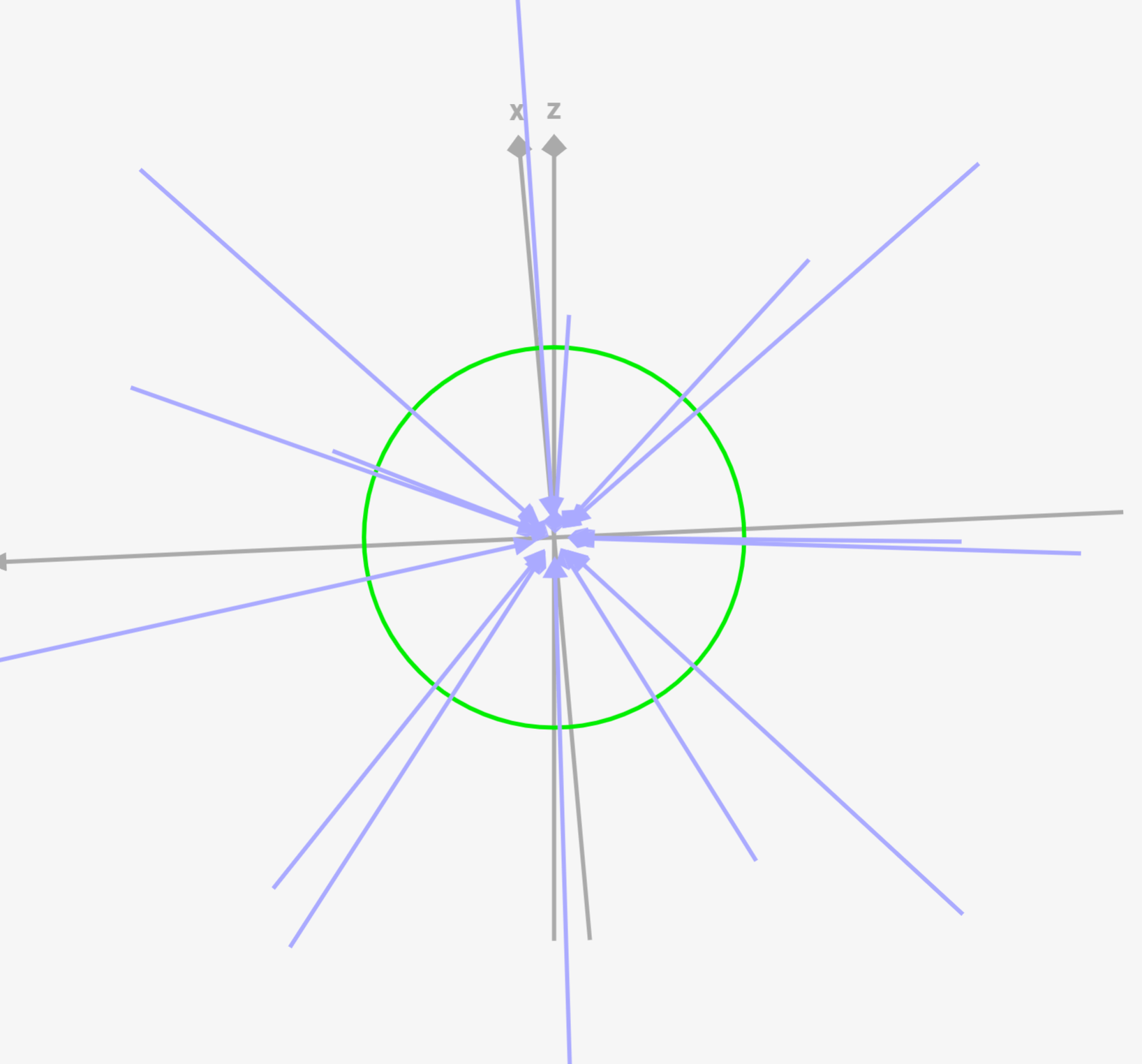
「力線が多くなる = 及ぼす力が大きくなる」と考えれば、見えないクーロン力がどういったものかイメージしやすくなると思います!
- 電荷から\(4πkq\)本の電気力線が発されると考えると、そこからの距離rによってクーロン力\(F = k \frac{|q_1||q_2|}{r^{2}}\)がかかるという事実とつじつまが合う(遠いほど電気力線の密度が下がる)
- 電荷に比例して電気力線の本数が上がっていき、クーロン力も強くなっていく
⇒「静電気・電場」カテゴリ記事一覧
その他関連カテゴリ
















