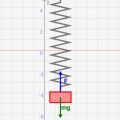
バネ振動(単振動)と円運動の関係をシミュレーションで理解しよう![物理入門]
前回の記事で、バネにモノをつけるとその初期位置によって振動が起こるということを解説しました。バネは位置によって加わる力Fが変わるので、それによって振動が起きるわけです。
今回はその振動の正体を「円運動との関係」を考察して導いていきます!
![バネ振動(単振動)と円運動の関係をシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/rapture_20210519220325-300x500.jpg)
目次
おさらい:バネによる力の法則
まずはおさらいです。バネの力は↓のような力が働きます。
バネによる力 \(F = -kx\)
- k : バネ定数
- x : バネの自然長からの変位[\(m\)]
↓バネからの変位によって縮まる力・押す力が決まります。
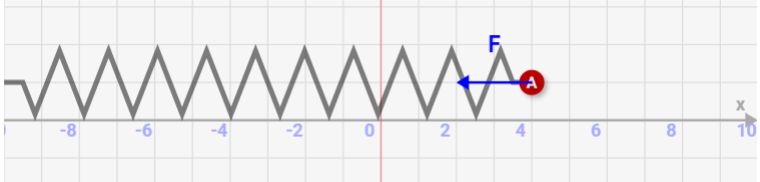
↓「自然長からの変位が2倍 ⇒ 力が2倍」になります。これがバネによって働く力です!
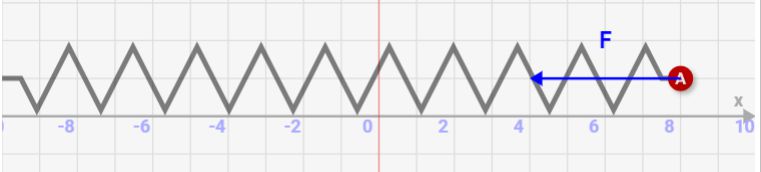
「バネによる力」と「円運動時の加速度」を比較してみる!
「バネによる力」と「円運動時の加速度」比較
ここで、上記の「バネによる力」と「円運動時の加速度」を比較して考えてみます。「円運動時の加速度」はコチラのページで詳しく解説していますので、今回は結果だけ引用します。
円運動の加速度は↓の形式で表せます。
\( a_x = – rw^2 \ cos(wt) = -w^2 \ x \)
\( a_y = – rw^2 \ sin(wt) =-w^2 \ y \)
- r : 円半径
- w : 角速度
ma=Fの関係が成り立つので、物体にかかる力Fは↓のようになります。
\( F_x = m a_x = -mw^2 \ x \)
\( F_y = m a_y = -mw^2 \ y \)
- m : 物体の質量
- w : 角速度
これは、バネの力「F = -kx」と形が一緒なんです!かかる力は一緒。なので実は、「円運動のx方向の動き」と「バネ振動の動き」は同一と言えるんです!
↓こんな対応関係です。バネ運動と円運動の横方向の動きと加わる力が一致しているんです。
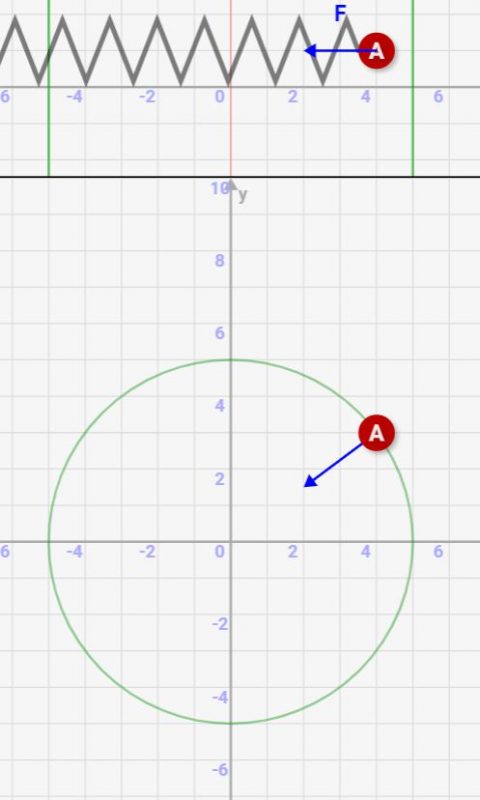
円運動の公式と比較してみる
では、どのような対応関係になるんでしょうか。
↓のような比較になるので
バネ振動:\(F = -kx\)
↓のような対応関係になります。
\( k = mw^2 \)
↓変形
\( \large{w = \sqrt{\frac{k}{m}}} \)
- k : バネ定数
- m : 物体の質量[kg]
つまり、「バネ振動 = 角速度\(\sqrt{\frac{k}{m}}\)で回転する円運動のx方向の動き」と言えるんです。このように「\(F = -kx\)で表せる形の運動」を「単振動」といいます。
シミュレーターで「バネ振動(単振動)と円運動の関係」を確認しよう!
それでは上で説明した「バネ振動(単振動)と円運動の関係」をシミュレーターで実際に確認しましょう!「円運動のx方向の動き」と「バネ振動」が完全に一致することを確認しましょう。
- スライドバーによって変位x,バネ定数k,物体の質量mが変えられます
- 指定した設定を初期値として、物体がバネの力で振動を開始します
- 同時に対応する円運動が下に描かれます
- バネ振動・円運動でかかる力は青色矢印で示されます
- 円運動とバネ振動で「物体の位置/速度/かかる力F」がx方向で一致することを確認しましょう
- シミュレーターの下にあるスライドバーで再生速度を変えられるので、スロー再生にしてみると、一致してることが分かりやすくなります
↓スライドバーを変化させて実験してみましょう!
円運動の性質から分かるバネ振動(単振動)の性質!
上記の通り、「円運動のx方向の動き」と「バネ振動の動き」は角速度\(w=\sqrt{\frac{k}{m}}\)という対応関係で一致します。ここから、↓のようなバネ振動の周期等を計算できます。
↓円運動の周期の公式にあてはめると、、、
\( \displaystyle 周期T = \frac{2 \pi}{角速度w} = 2 \pi \sqrt{\frac{m}{k}} \)
↓円運動の速度の公式に当てはめると、、、
\(\displaystyle 円運動のx方向速度 = – rw \ sin(wt) \)
\(\displaystyle = – x_0 \sqrt{\frac{m}{k}} sin(\sqrt{\frac{m}{k}} t) \)
となります。このように、円運動と比較することで、バネ振動がどのような動きをするのかが丸わかりになるんです!
- バネ振動と円運動は横から見ると、実は全く同じ動きをする
- バネ係数kと物体の質量mによって回転速度が決まる
⇒「円運動」カテゴリ記事一覧
⇒「単振動(バネ運動)」カテゴリ記事一覧
その他関連カテゴリ