「ド・モアブルの定理」をシミュレーターで理解しよう![数学入門]
このページでは複素数について、分かりやすく解説しています!
今回は「ド・モアブルの定理」をシミュレーターを用いて分かりやすく説明します!
![「ド・モアブルの定理」をシミュレーターで理解しよう![数学入門]](https://retu27.com/wp-content/uploads/20220306121544-500x500.png)
おさらい:虚数、複素数とは
複素数とは
実数+虚数の組み合わせを一つにしたものを複素数といいます。
複素数 = 実数と虚数の組み合わせ
例えば「+1.9 + 2.9i」という形です。
複素数は↓のように二次元のグラフで表現します。これを複素数平面といいます。
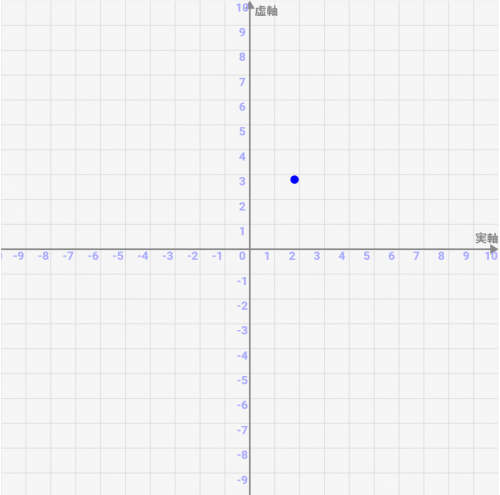
複素数のもう一つの表し方:極形式
複素数はその他にも複素数を表すための方法があるんです。それが極形式になります!
複素数を↓のように絶対値rと偏角(角度)θであらわしたもの
複素数z = \(r(cosθ + i \ sinθ)\)
コチラのページでも解説していますが、三角関数cosとsinを使えば、↑のように半径rと角度θで位置を表せるんですね。
また、複素数の場合はこの角度を偏角といいます!
複素数の乗算
↓のように二つの複素数 \(z_1\)と\(z_2\)の乗算を考えます。
\( z_2 = r_2(cosθ_2 +i \ sinθ_2)\)
加法定理を使うと↓のように計算できます
\( = r_1r_2\{cos(θ_1+θ_2)+i \ sin(θ_1+θ_2)\}\)
つまり、複素数の乗算は「絶対値は乗算」「偏角は足し算」という演算になるんです!
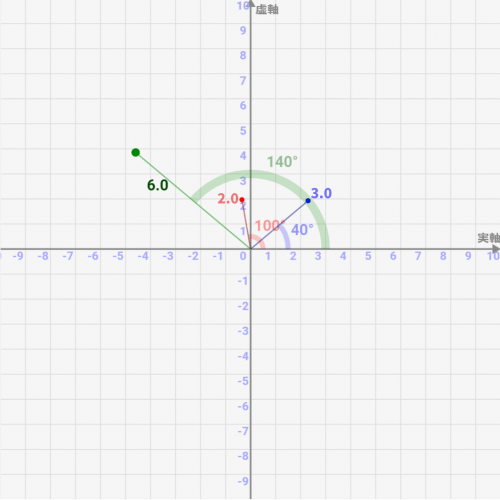
具体的に\(z_1\)を赤色、\(z_2\)を青色として、乗算したものを緑色で示したのが↓になります。
絶対値(長さ)は掛け算されて、2.0*3.0=6.0となります。
それに対して角度は100+40=140°と足し算なるんですね!
ド・モアブルの定理
ド・モアブルの定理は↓の式が成り立つという定理です
\((cosθ+ i \ sinθ)^n=cos(nθ)+ i \ sin(nθ)\)
これは、↑で解説した複素数の乗算を考えれば簡単です。絶対値=1なので↓のように定式化できます。
これを帰納法で証します。
n=1が成り立つのは自明ですね。
次にn=kが成り立つとして、n=k+1のときを考えると
↓複素数の乗算は、偏角の足し算
\( z^{k+1} = (cos(kθ+θ) +i \ sin(kθ+θ)) \)
\( = cos(k+1)θ +i \ sin(k+1)θ \)
となるため、k+1の時も成り立ちます。
故に、↑のド・モアブルの定理は当たり前のように成り立ちます!
「ド・モアブルの定理」をシミュレーターで理解しよう!
それでは解説してきた、「複素数の乗算」をシミュレーターで確認してみましょう!↓の形でθとnを指定すると、n乗した複素数を表示します!
- 複素数のθとnを指定すると、\(z^n\)を計算します
- \(z\)を青色、そして乗算結果\(z^n\)は緑色で示しています
\(z^n\) = (cos()+i sin())
- 絶対値1の複素数は、n乗するのはn倍回転するのに等しい
⇒「複素数」カテゴリ記事一覧
その他関連カテゴリ















