「複素数の極形式への変換」をシミュレーターで理解しよう![数学入門]
このページでは複素数について、分かりやすく解説しています!
今回は「複素数の極形式への変換」をシミュレーターを用いて分かりやすく説明します!
![「複素数の極形式への変換」をシミュレーターで理解しよう![数学入門]](https://retu27.com/wp-content/uploads/20220306093054-500x500.png)
目次
おさらい:虚数、複素数とは
複素数とは
実数+虚数の組み合わせを一つにしたものを複素数といいます。
複素数 = 実数と虚数の組み合わせ
例えば「+1.9 + 2.9i」という形です。
複素数は↓のように二次元のグラフで表現します。これを複素数平面といいます。
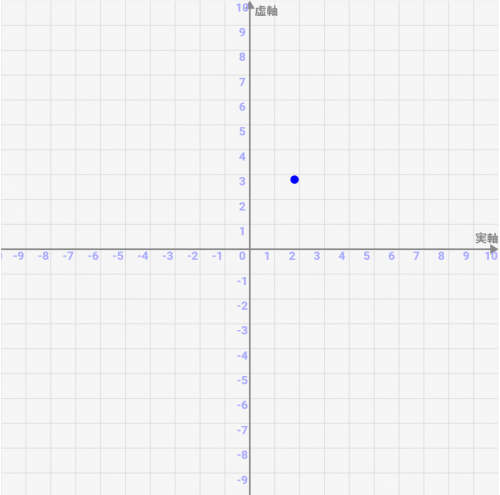
複素数のもう一つの表し方:極形式
複素数はその他にも複素数を表すための方法があるんです。それが極形式になります!
複素数を↓のように長さrと偏角(角度)θであらわしたもの
複素数z = \(r(cosθ + i \ sinθ)\)
コチラのページでも解説していますが、三角関数cosとsinを使えば、↑のように半径rと角度θで位置を表せるんですね。
また、複素数の場合はこの角度を偏角といいます!
例えばr=7,θ=30°だった場合は↓のようになります。
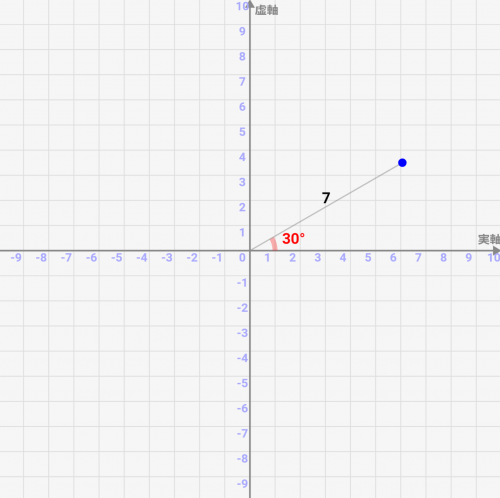
標準形の複素数から、極形式への変換
↑にように複素数は2パターンで表せます。この変換は以下のようにしていけば出来ます。
今、標準形を↓のように実数部をa,虚数部をbと表すことにします。
\( z = a + bi\)
極形式の長さ(絶対値)
長さrについては、円の半径と同じく↓の公式で求められます。極形式ではこれを絶対値といいます。
\( r = \sqrt{a^2 + b^2} \)
これは↓のような図になることを考えれば自明ですよね。

cosθ+ i sinθ部分
cosθ+ i sinθの部分は絵にすると、↓のようになります。斜め線の長さが\( r = \sqrt{a^2 + b^2} \)になるので、「cos=横線/斜め」と「sin=縦線/斜め」という定義を用いれば↓のようになります。

\(\displaystyle cosθ = \frac{a}{r} = \frac{a}{\sqrt{a^2 + b^2}}\)
\(\displaystyle sinθ = \frac{b}{r} =\frac{b}{\sqrt{a^2 + b^2}}\)
cosθとsinθがわかるので、θはここから計算できるはずなんです。
最終的な極座標への変換
↑の論議をまとめると、最終的な極座標への変換は↓のようになります。
\( 複素数z = a + bi \)
\(\displaystyle = r(cosθ + i \ sinθ) \)
\(\displaystyle = \sqrt{a^2 + b^2}(\frac{a}{\sqrt{a^2 + b^2}} + \frac{b}{\sqrt{a^2 + b^2}}i) \)
実際に計算すると、極形式も標準形も同じ値になることがわかります!
「複素数の極形式への変換」をシミュレーターで理解しよう!
それでは解説してきた、「複素数の極形式への変換」をシミュレーターで確認してみましょう!↓の標準形aとbの値を指定すると、極座標に変換するものです。
\( z = a + bi\)
- ↓で標準形の実数aと虚数bをそれぞれ指定できます
- 指定した標準形の複素数が、どのような極形式になるか確認してみましょう
- ↑で説明した式の通りに変換されていることを確認しましょう!
z = (cos()+i sin())
- 標準形から極形式へは図形的に考えれば変換できる
- 極形式も計算すれば標準形の「a + bi」という形に戻せるため、2つの表記法は同値であるといえる
⇒「複素数」カテゴリ記事一覧
その他関連カテゴリ















