数学的帰納法の考え方/実例をアニメーションで理解しよう![数学入門]
本記事では数学的帰納法という証明方法を解説していきます!
![数学的帰納法の考え方/実例をアニメーションで理解しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200613205623-500x177.jpg)
目次
数学的機能法の考え方
数学的帰納法を説明するために、前回のΣ記号の記事で紹介した以下の式の証明を考えていきます。
\( \displaystyle \sum_{i=1}^{n}(i) = \frac{1}{2}n(n+1) \)
前回は、等差数列の公式を用いたりして証明していましたが、、
実は以下の2点を確認することだけで、証明可能なんです。これが数学的帰納法です!
1. n=1で式が成り立つ
2. n=kで成り立つ時、n=k+1でも式が成り立つ
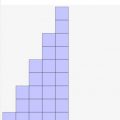
上記の2つさえ示せれば、任意の自然数nで上記式が成り立つと言えます。これは、以下のようなアニメーションイメージで考えると分かりやすいです。
上図はn=1,2,…,5の時に上記式を証明していく過程を表したものです。これら全てで成り立つのを示すために、まず「1. n=1で式が成り立つ」ということを証明します。そして、その後は「2. n=kで成り立つ時、n=k+1でも式が成り立つ」という式を適用すると、次々に右隣の数でも成り立つことが示していけます。結局、無限大までこのように連鎖的に証明できますので、任意の自然数nに対して式が成り立つと言えるわけです。
それでは以下、前回説明したシグマに関する公式の証明を、数学的帰納法を使って再度証明してみます!
数学的帰納の例1:\(Σk\)の例
それでは上記でも出てきた
\( \displaystyle \sum_{i=1}^{n}(i) = \frac{1}{2}n(n+1) \)
の式について、2段階で証明していきます!
証明手順1.n=1で式が成り立つ
これは代入すればすぐ示せます。
\( \displaystyle \sum_{i=1}^{n}(i) = \sum_{i=1}^{1}(i) = 1\)
\( \displaystyle \frac{1}{2}n(n+1) = \frac{1}{2}(1+1) = 1\)
両辺ともに1なので成立します。
2. n=kで成り立つ時、n=k+1でも式が成り立つ
前提が「n=kで成り立つ」なので、
\( \displaystyle \sum_{i=1}^{k}(i) = \frac{1}{2}k(k+1) \)
が成立していると仮定できます。
このとき、n=k+1の式を考えると
\( \displaystyle \sum_{i=1}^{k+1}(i) \)
\( = \displaystyle \sum_{i=1}^{k}(i) + (k+1) \)
↓n=kの時の式を代入
\( = \displaystyle \frac{1}{2}k(k+1) + (k+1) \)
\( = \displaystyle \frac{1}{2}\{k(k+1) + 2(k+1)\} \)
\( = \displaystyle \frac{1}{2}(k+1)(k+2) \)
と変形できます。
これは証明式の右辺にn=k+1を代入した式と同等であり、n=k+1のときも証明式が成立したと言えます!
これで数学的帰納法に必要な2点が成立することを証明しました。このため、↓のアニメーションのように、最終的には全ての自然数nで上記式が成立すると言うことができます!
数学的帰納の例2:\(Σk^2\)の例
上記と同様に、もう一つの\(Σk^2\)の場合の公式
\( \displaystyle \sum_{k=1}^{n}(k^2) = \frac{1}{6}n(n+1)(2n+1) \)
を証明していきます!
証明手順1.n=1で式が成り立つ
これは代入すればすぐ示せます。
\( \displaystyle \sum_{i=1}^{n}(i^2) = \sum_{i=1}^{1}(i^2) = 1\)
\( \displaystyle \frac{1}{6}n(n+1)(2n+1) = \frac{1}{6}(2 \cdot 3) = 1\)
両辺ともに1なので成立します。
2. n=kで成り立つ時、n=k+1でも式が成り立つ
前提が「n=kで成り立つ」なので、
\( \displaystyle \sum_{i=1}^{k}(i^2) = \frac{1}{6}k(k+1)(2k+1) \)
が成立していると仮定できます。
このとき、n=k+1の式を考えると
\( \displaystyle \sum_{i=1}^{k+1}(i^2) \)
\( = \displaystyle \sum_{i=1}^{k}(i^2) + (k+1)^2 \)
↓n=kの時の式を代入
\( = \displaystyle \frac{1}{6}k(k+1)(2k+1) + (k+1)^2 \)
\( = \displaystyle \frac{1}{6}\{k(k+1)(2k+1)+ 6(k+1)^2\} \)
\( = \displaystyle \frac{1}{6}\{(k+1)(2k^2+k+6k+6)\} \)
\( = \displaystyle \frac{1}{6}\{(k+1)(2k^2+7k+6)\} \)
\( = \displaystyle \frac{1}{6}(k+1)(k+2)(2k+3) \)
\( = \displaystyle \frac{1}{6}(k+1)(k+2)(2(k+1)+1) \)
と変形できます。
これは証明式の右辺にn=k+1を代入した式と同等であり、n=k+1のときも証明式が成立したと言えます!
このため、1つ目の例と同様に、最終的には全ての自然数nで上記式が成立すると言うことができます!
↓この順々に式が成立するイメージを掴んで起きましょう!
- 数学的機能法は「1. n=1で式が成り立つ」「2. n=kで成り立つ時、n=k+1でも式が成り立つ」の2つを示せば証明できる
- 証明はn=kの時成り立つ前提の式を使い、n=k+1でも成り立つことを証明できれば良い
⇒「数列」カテゴリ記事一覧
⇒「数学」カテゴリ記事一覧
その他関連カテゴリ