等速円運動を速度・加速度の変化をシミュレーターで観察して、理解を深めよう![物理入門]
前回の記事で、等速円運動をx,y座標に分けて、定式化して解説しました。
今回は、そのx,yの式を使って、等速円運動の速度・加速度の式を微分を使って求めて行きます!
![等速円運動を速度・加速度の変化をシミュレーターで観察して、理解を深めよう![物理入門]](https://retu27.com/wp-content/uploads/rapture_20210516141206-500x500.jpg)
目次
おさらい:等速円運動のx座標はcos,y座標はsinで表現できる!
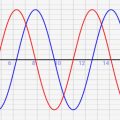
まず前回のおさらいからです。前回シミュレーターを交えて解説した通り、半径r/角速度wの等速円運動のx,y座標は↓のように計算できます。
\( x \displaystyle = r \ cos(wt) \)
\( y \displaystyle = r \ sin(wt) \)
*初期角度はθ=0(rad)とする
- r : 半径[m]
- w : 角速度[rad/s]
↓の赤線がx座標、青線がy座標の動きです。このように角座標はcos/sinに従って動くんですね!

「速度」「加速度」を微分を使って求める!
円運動の速度の求め方
上記の式で、等速円運動のx,y座標が求まりました。以前の記事で解説したとおり、x,y座標の式が求まっていれば、それを微分することで速度が求まり、さらにもう一回微分すると加速度が求まります!この通りに求めていってみましょう。

再掲になりますが、x,y座標は↓のようになるので、、、これを微分します。
\( x \displaystyle = r \ cos(wt) \)
\( y \displaystyle = r \ sin(wt) \)
*初期角度はθ=0(rad)とする
- r : 半径[m]
- w : 角速度[rad/s]
cos,sinの微分はコチラのシミュレーターで解説している通りで↓になります。
\( (cos(x))’ = - sin(x) \)
\( (sin(x))’ = cos(x) \)
さらに、合成関数の微分を考えると、x=wtとすれば、\(\large{\frac{dy}{dt}=\frac{dy}{dt} \frac{dx}{dt}}\)なので↓のようになります。
\( (cos(wt))’ = - w \ sin(wt) \)
\( (sin(wt))’ = w \ cos(wt) \)
これに半径rを乗算すれば、円運動の速度\(v_x,v_y\)が求まります!
\( v_x = (r \ cos(wt))’ = - rw \ sin(wt) \)
\( v_y = (r \ sin(wt))’ = rw \ cos(wt) \)
角座標の速度は求まったので、最終的な速度の大きさを計算すると、↓のようにv=rwになります。角速度の定義通りの結果になりました!
\( v = \sqrt{{v_x}^2 + {v_y}^2} \)
\(= \sqrt{r^2w^2({sin(wt)}^2 + {cos(wt)}^2)} = rw \)
円運動の加速度の求め方
加速度についても、同じように\(v_x,v_y\)を微分すれば求まります。
速度は↓で表せるので。
\( v_x = (r \ cos(wt))’ = - rw \ sin(wt) \)
\( v_y = (r \ sin(wt))’ = rw \ cos(wt) \)
これを同様に微分すると加速度(\(a_x,a_y\))は↓のようになります。
\( a_x = (- rw \ sin(wt))’ = - rw^2 \ cos(wt) \)
\( a_y = (rw \ cos(wt))’ = -rw^2 \ sin(wt) \)
ここで、\(x=r \ cos(wt)\)、\(y=r \ sin(wt)\)なのでこれを代入すると、、
\( a_x = – rw^2 \ cos(wt) = -w^2 \ x \)
\( a_y = -rw^2 \ sin(wt) =-w^2 \ y \)
となります。つまり、加速度はx,yの定数倍(\(-w^2\))になるんです!ただし、マイナスなのでx,yとは逆になります。
また。角座標の加速度は求まったので、最終的な加速度の大きさを計算すると、↓のようにa=\(rw^2\)になります。これも重要なので覚えておきましょう!
\( a = \sqrt{{a_x}^2 + {a_y}^2} \)
\(= \sqrt{r^2w^4({cos(wt)}^2 + {sin(wt)}^2)} = rw^2 \)
等速円運動を速度・加速度シミュレーターで理解しよう!
上記のように微分を使って求めただけだと、イメージがわかないですよね。そのため、速度と加速度がわかるシミュレータを用意しました!
- ↓のスライドバーで円の半径と角速度(rad/s)を自由に変更できます
- シミュレーターの上で速度を青矢印、加速度を赤矢印で示します
- 入力を変えて、速度、加速度がどのように変わるのか観察しましょう
シミュレーター結果解説
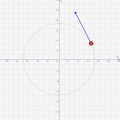
↓の絵のように「速度は円の接線となる方向」となり、「加速度は中心に向かう方向」に向かいます。

そして、↑の考察の通り、角速度wが増加すると速度はw倍になり、角速度は\(w^2\)倍と急増します。

まとめ:円運動の速度・加速度は微分をしていくことで求められる!
上記の経過のとおり、円運動の速度、加速度は↓のx,y座標をもとに微分していくと↓のように求められます。
\( v_x = (r \ cos(wt))’ = - rw \ sin(wt) \)
\( v_y = (r \ sin(wt))’ = rw \ cos(wt) \)
- r : 半径[m]
- w : 角速度[rad/s]
\( a_x = (- rw \ sin(wt))’ = - rw^2 \ cos(wt) \)
\( a_y = (rw \ cos(wt))’ = -rw^2 \ sin(wt) \)
また、↑の絵のように速度は接線方向に、加速度は中心に向かうようにかかることが重要です!
ただ、「なんで中心に加速度が発生しているの?別に中心に物体は移動していないのでは?」って直感的には思ってしまいますよね。そこで次回は、直感的に円運動の速度・加速度がわかるようなシミュレーターを使って直感的な理解を深めていこうと思います!
- 円運動の速度は、円の接戦方向となる
- 円運動の加速度は、円の中心に向かう
⇒「円運動」カテゴリ記事一覧
その他関連カテゴリ