「弧度法・ラジアン」とは何かをシミュレーターで解説します！[数学・物理入門]

2021-05-15　 三角比・三角関数,円運動

今回は、sin/cos等の三角関数や、物理の円運動の基礎として「弧度法・ラジアン」について説明します。数学・物理の世界では角度を360度という度数表記でなく、2πとラジアン形式で表すことが多いです。

今回は基礎固めのために、この「弧度法・ラジアン」について詳しく説明します！

ラジアンの定義

まず、ラジアンの定義を紹介します。

文の定義だと分かりにくいですね。絵で書くと1radは↓のようになります。「弧」とは、「円周上の線」という意味です。弧が半径の長さと等しくなったとき、、、そのときの角度を1radと呼んでいるんですね！

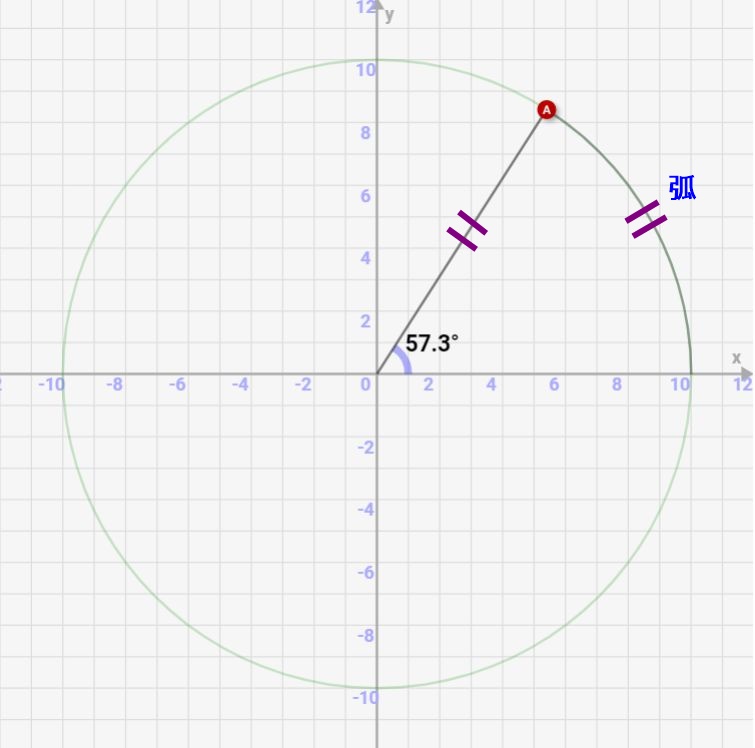
具体的にいうと1radは

です。中途半端な数字ですが仕方ないのです、、、＞＜

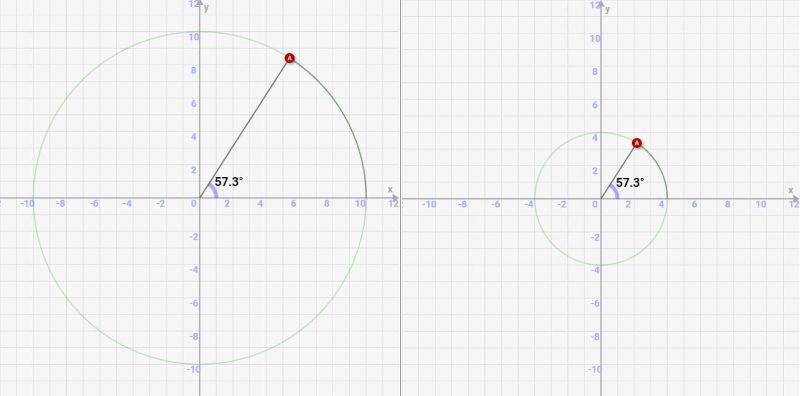
1radは半径が変わっても、角度は変わらない

当然のことですが、1radは円の半径が変わっても角度は変わらず約57.3度です。円は半径が違っても相似関係にあるため、半径がA倍になったら、弧もA倍になります。なので↓のように1radの角度はどんな大きさの円でも変わりません！

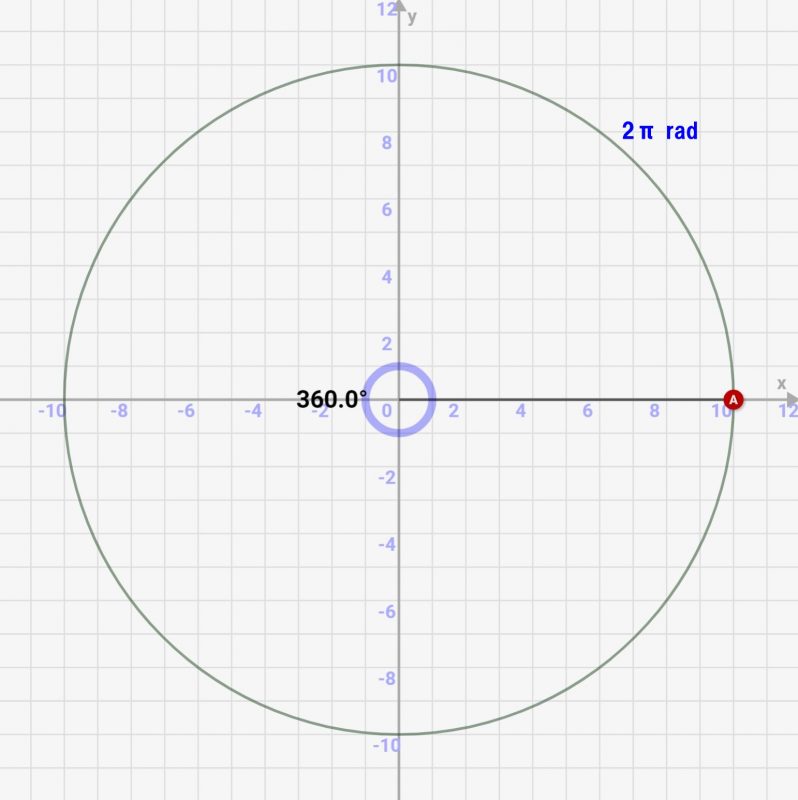
360度＝2π rad

rad表示で確実なのは「1周(360度)は2\(\pi(rad)\)」になることです。

なぜなら、円周は小学校で習う通り、「円周＝半径*2\(\pi\)」です。今、半径＝1radなのでこれを代入すると、「円周＝2\(\pi\) rad」になります。つまり、「\(\pi\) rad=180度」です！

　

ラジアン⇔度数変換方法

上記の定義に基づくと、ラジアンと度数の間の変換は↓のようになります。\(180(度)=\pi(rad)\)の関係が成り立つので、この関係を使って変換できます！

主な角度は、↓のような対応関係にあります。この対応関係はよく使うのでパッと変換できるようにしておきましょう！

弧度法・ラジアンをシミュレーターで度数との対応関係を確認しよう！

それでは実際にシミュレーターで弧度法・ラジアンを確認してみましょう！

まとめ：数学・物理では1周を2πとするradで角度を表現します！

今回説明してきたとおり、数学・物理等の世界では角度を360度表記でなく、ラジアン(rad)で表現します。その定義は、「1rad = 半径rと同じ長さの弧がなす角度」です。

↓の対応関係を覚えておき、いつでも度数⇔ラジアンで変換できるようにしておくことが重要です！必ず覚えておきましょー！

[関連記事] 等速円運動

1．弧度法・ラジアン(本記事)

2．角速度

3．周期・回転数

4．円運動のx,y座標を求める

5．円運動を速度・加速度(微分で求める)

6．円運動の速度・加速度を直感的に求める