等速円運動をx,y座標の動きをシミュレーターで観察して、理解を深めよう![物理入門]
前回の記事までで「角速度」について解説してきました。今回はそれを前提に「等速円運動をどのように方程式に落とせばよいか」を考えていきます。
そのために「円運動をx,y座標に分けて考える」ということが必要です!
![等速円運動をx,y座標の動きをシミュレーターで観察して、理解を深めよう![物理入門]](https://retu27.com/wp-content/uploads/rapture_20210516122453-500x248.jpg)
目次
等速円運動のx座標はcos、y座標はsinに従った動きをする!
等速円運動のx,y座標の動きをシミュレーターで観察してみよう!
円運動をx,y座標に分けて考えてみます。そのときにx,yがどのような動きをするかを↓のシミュレーターで確認してみましょう!
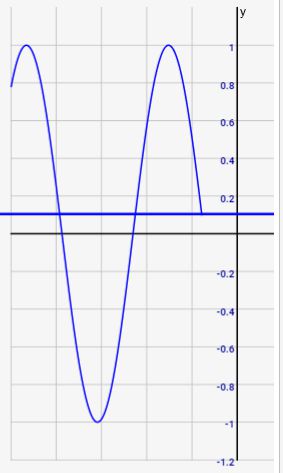
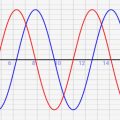
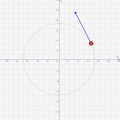
- 左上に単位円があり、右側の青い線がy座標の動き,下側の赤い線がx座標の動きに対応しています
- x座標は描画の都合上、90度回転して表示しています
x座標はcos、y座標はsinに従った動きをする
シミュレーターでみると分かりやすいですが、x,y座標はそれぞれcos/sinの動きに従って動きます。
そもそも、cos/sinの定義が「↓のような単位円でxがcos、yがsin」というものなので、これは当たり前のことなんです。

全体でみると物体は等速だが、x,y座標でみると加速・減速している!
もうひとつ重要なのが、「x,y座標でみると物体は加速・減速を繰り返している」ということです。
これは↓をみても自明です。重要なのは「等速円運動でも、方向を変えるために加速・減速を繰り返している」ということです。直線で等速運動するのと違って、等速円運動では方向を変えるために加速・減速するんです。
x,y座標を半径r、角速度wをつかって表現する
↑のシミュレーターの通り、円運動のx,y座標はcos/sinに従うことは分かりました。これを定式化してみましょう!
まず、時刻tでの角度θを求める必要があります。これは、t=0の角度をθ=0とする前提にすると、↓のように求められます。1秒間でw(rad)回転するので、時刻t時点ではθ=wtになります。
\( θ(rad) \displaystyle = wt \)
- w : 角速度[rad/s]
これを前提に、半径rの円を考えるとx,y座標は↓のように定式化できます。半径r上の円であり、θ=wtのため、このように定式化できるのです!
\( x \displaystyle = r \ cos(wt) \)
\( y \displaystyle = r \ sin(wt) \)
- r : 半径[m]
- w : 角速度[rad/s]
シミュレーターで等速円運動のx,y座標の動きを観察しよう!
それでは実際にシミュレーターで「等速円運動のx,y座標」の動きを確認してみましょう!
- ↓のスライドバーで円の半径と角速度(rad/s)を自由に変更できます
- シミュレーターの上で赤線をx座標、青線をy座標で示します
- シミュレーターの下にx,y座標の時系列変化をグラフ化して表示しています
- グラフ化したx,y座標がcos,sinが、半径rと角層度wを変えるとどう変化するか確認しましょう
↓赤線がx座標、青線がy座標
シミュレーター結果
シミュレーターを動かすと、↓のようにグラフ化されることがわかると思います。赤線がcos,青線がsinになっていることがわかりますね。

この振幅は半径rによってきまります。半径r=2にすると↓のように振幅が下がります。
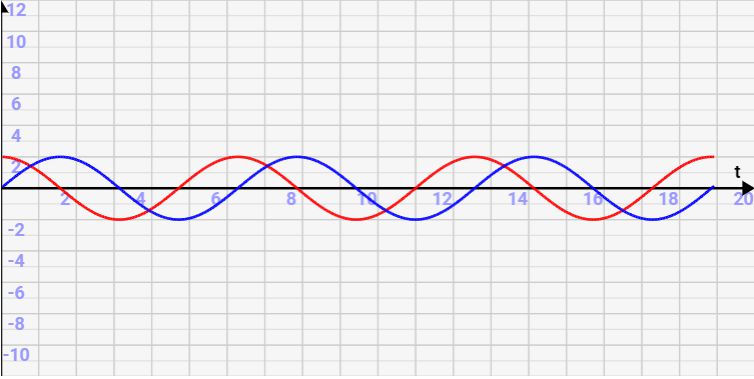
また、円運動の回転数は角速度に比例します。角速度を2倍にすると↓のように、回転数が2倍となり、周期が半減します!

このように、x,y座標のグラフの形は半径rと角速度wで決まるんですね!
まとめ:等速円運動はx,y座標に分けて考えられる
上記の考察とシミュレーションの結果の通り、等速円運動は↓のように定式化できます。つまり、半径rと角速度wによってグラフの形が変わります。
\( x \displaystyle = r \ cos(wt) \)
\( y \displaystyle = r \ sin(wt) \)
- w : 角速度[rad/s]
*初期角度はθ=0(rad)とする
等速円運動のx,y座標がこのように決まったので、これを微分していけば、円運動の速度と加速度が求められるはずです!ということで次回の記事では、「等速円運動時の速度・加速度」について考察していきます!
- 等速円運動はx,yに分けると、cos,sinという三角関数で表現できる
- 等速円運動でも、x,yそれぞれで見ると減速と加速を繰り返している
⇒「円運動」カテゴリ記事一覧
その他関連カテゴリ