「二次方程式(二次関数)の虚数解」をシミュレーション/図解で理解![数学入門]
前回記事で、虚数とは何かを説明しました。また、コチラの記事では二次方程式の解の公式について説明し、場合によって解が0,1,2個とかわることを説明しました。
今回は虚数を使って、「二次方程式(二次関数)の虚数解」について説明します!
![「二次方程式(二次関数)の虚数解」をシミュレーション/図解で理解![数学入門]](https://retu27.com/wp-content/uploads/20220305211812-470x500.png)
目次
おさらい:二次関数の「解の公式」「解の判別式」
前回記事のとおり、二次方程式の解は↓の式で求められます。
$$ { x = \frac{ -b \pm \sqrt{b^2 -4ac}}{2a}} $$
ただし解が本当にあるかは↓の判別式をみないといけません。この判別式Dは↑の解の公式のルート内の式です。このルート部分が正か負かを判定することで解が何個あるかが決まるという事です!
\(\Large{D=b^2 -4ac}\) としたとき、
D < 0 ⇒ 解無し(二次関数はx軸と交わらない)
D = 0 ⇒ 解1つ(二次関数とx軸が接する)
D > 0 ⇒ 解2つ(二次関数とx軸が交わる)
虚数を認めれば、ルートの中がマイナスでも解はある!
↑の論議は「実数」という前提の話でした。しかし、虚数iをつかうと解がいつでも出てくるんです!
ルート内がマイナスの場合の解
しかし、前回記事で話したように仮想的に↓の虚数iという数を考えると、、、
虚数i = 二回かけると-1になる仮想的な数
\(i*i = -1\)
↑の式にルートをとると↓のようになります。
\( \sqrt{i*i} = \sqrt{-1} \)
\( i = \sqrt{-1} \)
つまり、マイナス数のルートは存在しないという前提でしたが、虚数まで含めると解が存在するんです!例えば↓の例のようにルート内の解が得られるんです!
\( D= 2^2 -4*1*2 = -4 \)
\(\sqrt{D}=\sqrt{-4}=\sqrt{-1}*\sqrt{4}=i*2\)
↓方程式の解
\( \displaystyle x = \frac{-2 \pm 2i}{2} = -1 \pm i \)
実際に↑の例の二次曲線は↓のようになります。x軸に接さず、実数解は存在しない事がわかります。
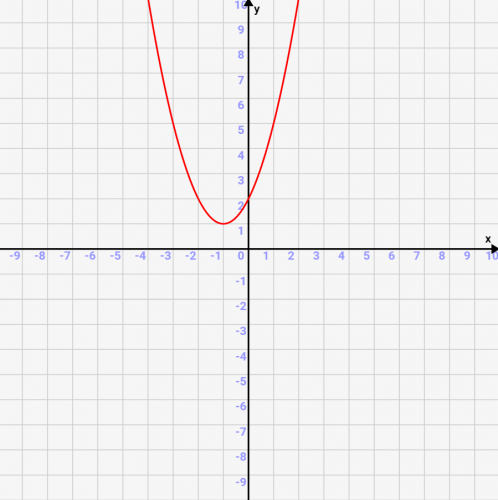
つまり、虚数を含めた場合、解の数は↓のようになります。Dがマイナスになったときに、虚数解が2つ出現するイメージです!
\(\Large{D=b^2 -4ac}\) としたとき、
D < 0 ⇒ 虚数解2つ(二次関数はx軸と交わらないが虚数解有り)
D = 0 ⇒ 解1つ(二次関数とx軸が接する)
D > 0 ⇒ 実数解2つ(二次関数とx軸が交わる)
「二次方程式(二次関数)の解(虚数含む)」をシミュレーターで理解しよう!
それでは解説してきた、「虚数解込みの二次奉呈式の解」の考え方をシミュレーターで確認してみましょう!
\(\large{y = ax^2 + bx + c}\)という二次関数をシミュレートできます!
- ↓でa,b,cを指定すると、二次関数がグラフ表示されます
- x軸との交点(y=0解の位置)を青点で示しています
- 解xが↑で説明した虚数含めた解の公式に当てはまっていることを確認しましょう
- 判別式Dの符号によって、虚数解か実解か決まることを確認しましょう
- 虚数解の場合は、実際には二次曲線はx軸に触れないことを確認しましょう
\( {y=} \) + 1\( {x^2 } \) + 1\( {x } \) + 1
[解]
解の判別式: D=\(b^2 -4ac=\)
解の個数: 0
解: x = 0
まとめ
二次方程式は、実数解のみ考えうる場合は↓のような判別となっていました。これは、ルートの中がマイナスになった場合に解がとれないからです。
\( \large{D=b^2 -4ac} \) としたとき、
D < 0 ⇒ 解無し(二次関数はx軸と交わらない)
D = 0 ⇒ 解1つ(二次関数とx軸が接する)
D > 0 ⇒ 解2つ(二次関数とx軸が交わる)
しかし、「虚数\(i=\sqrt{-1}\)」なのでこれを使うと必ず解が得られるようになるため、↓のような判別式にかわります。
\( \large{D=b^2 -4ac} \) としたとき、
D < 0 ⇒ 虚数解2つ(二次関数はx軸と交わらないが虚数解有り)
D = 0 ⇒ 解1つ(二次関数とx軸が接する)
D > 0 ⇒ 実数解2つ(二次関数とx軸が交わる)
虚数が入るか入らないかで、考え方や解の数がかわることを意識しましょう!
- 「虚数\(i=\sqrt{-1}\)」である
- 虚数解を許すと、二次方程式には必ず解がつくれる
⇒「二次関数」カテゴリ記事一覧
⇒「複素数」カテゴリ記事一覧
その他関連カテゴリ


















