tan)をシミュレーターで理解しよう！[数学入門]

2022-03-05　

三角関数sin/cos/tan

このページでは簡単に数学の関数の一つである三角関数(cos,sin)について、より分かりやすく解説しています！
今回は加法定理です。加法定理は別記事で解説する「倍角の公式」や「複素数平面」でものすごく意味を持つ強力な定理です！

シミュレーターでその意味を理解しておきましょう！

加法定理(cos/sin/tan)をシミュレーターで理解しよう！[数学入門]

1 加法定理とは
2 加法定理の証明
3 シミュレーターで加法定理が成り立つことを確認しよう！
- 3.1 加法定理(引き算)シミュレーター
- 3.2 加法定理(足し算)シミュレーター

加法定理とは

加法定理とは↓の3つの式のことを言います。cos/sin/tanに対してαとβを足し算/引き算が、求められるんです！

加法定理

$$ \displaystyle cos(α \pm β) = cosαcosβ \mp sinαsinβ $$ $$ \displaystyle sin(α \pm β) = sinαcosβ \pm cosαsinβ $$ $$ \displaystyle tan(α \pm β) = \frac{tanα \pm tanβ}{1 \mp tanαtanβ} $$

なぜこれが成り立つのかを以後説明していきます！

加法定理の証明

加法定理の証明は↓のように4つのステップを踏みます。ただ、一番需要なのは「step1: cos(α- β)式の証明」で、あとはそれを各式に展開するだけです。

step1: cos(α- β)式の証明　（最重要）
step2: cos(α+β)式への展開
step3: sin式への展開
step4: tan式への展開

step1: cos(α- β)式の証明

今、↓のように単位円上に角度αと角度βの角があるとします。今回はこの間の角「α – β」に着目します。

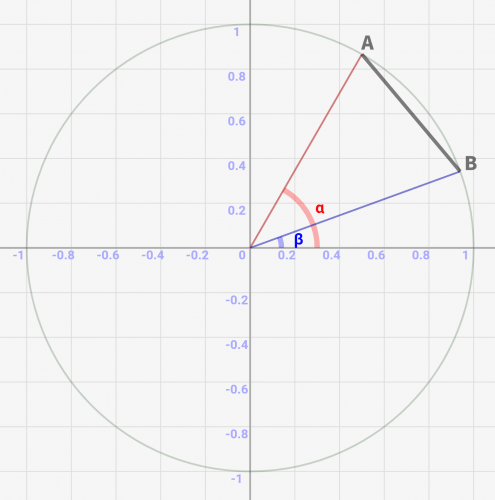
そして、この「α – β」を↓のように0度の位置まで回転させる事を考えます。

この時、あたりまえですが↑のABとCDの長さは同じになります。両方とも「α – β」と角度は同じで、ただ回転させただけですから！
そして、この「AB＝CD」をもとにすれば加法定理が求められるんです！

ABとCDをsin,cosを使って定式化すると↓のようになります。

$ AB^2 = (cosβ – cosα)^2 + (sinβ – sinα)^2 $
$ = cos^2β + cos^2α -2cosβcosα + sin^2β + sin^2α -2sinβsinα $
↓ $cos^2θ + sin^2θ = 1$の公式
$ = -2cosαcosβ -2sinαsinβ +2 $

$ CD^2 = (cos(α-β) – 1)^2 + sin^2(α – β) $
$ = cos^2(α-β) +1 -2cos(α-β) + sin^2(α – β) $
↓ $cos^2θ + sin^2θ = 1$の公式
$ = -2cos(α-β) +2 $

上記の考察の通り、AB=CDのはずなので

$ AB^2 = CD^2 $
$ -2cosαcosβ -2sinαsinβ +2 = -2cos(α-β) +2 $
↓整理
$ cos(α-β) = cosαcosβ + sinαsinβ $

となりcos(α- β)の加法定理が証明できます！

step2: cos(α+β)式への展開

コチラのページで解説している負角定理を使います。

負角定理

$ cos(-θ)= cos(θ)$
$ sin(θ) = – sin(θ)$

cos(α+β)を式変形していくと、、

$ cos(α+β) = cos(α-(-β)) $
↓マイナスの加法定理適応
$= cosαcos(-β) + sinαsin(-β)$
↓負角定理適応
$ = cosαcosβ \ – \ sinαsinβ $

という式が成り立ちます。故にcosについてまとめると↓の加法定理が成り立つと言えるんです！

$$ \displaystyle cos(α \pm β) = cosαcosβ \mp sinαsinβ $$

step3: sin式への展開

さらにコチラのページで解説した余角定理↓を使ってsinに変換してみます。

余角定理

$ sinθ = cos(90 – θ)$
$ cosθ = sin(90 – θ)$

これを使って$ cos(90 – (α \pm β))$を計算してみると、、

$ cos(90 – (α \pm β)) = cos((90 – α) \mp β)) $
$ = cos(90 – α)cosβ \pm sin(90 – α)sinβ$
↓負角定理で変換
$ = sinαcosβ \pm cosαsinβ$
↓$ sinθ = cos(90 – θ)$なので
$ sin(α \pm β) = sinαcosβ \pm cosαsinβ $

とsinについての式も導けます！

step4: tan式への展開

tanは$\large tanθ = \frac{sinθ}{cosθ}$なのでこれに↑で導出した式をいれればOKです！

$\large tan(α \pm β) = \frac{sin(α \pm β)}{cos(α \pm β)}$
↓ cosθとsinθの加法定理適応
$ \Large = \frac{sinαcosβ \pm cosαsinβ}{cosαcosβ \mp sinαsinβ} $
↓ cosαcosβで分母分子を割る
$ \Large = \frac{\frac{sinα}{cosα} \pm \frac{sinβ}{cosβ}}{1 \mp \frac{sinαsinβ}{cosαcosβ}} $
↓各項を$tanθ = \frac{sinθ}{cosθ}$で変換
$ \Large = \frac{tanα \pm tanβ}{1 \mp tanαtanβ} $

式を導出してる過程でcosαcosβで割っているのを見ればわかる通りですが、cos＝0となるα＝90度 or β=90度の時にはtanの加法定理は直接計算できないため、純粋にcosとsinから算出したほうが良いです。

このように、cosに関する公式に余角定理などを適応していけばsin,tanの式も導けるんです！

シミュレーターで加法定理が成り立つことを確認しよう！

加法定理(引き算)シミュレーター

まず↓のαとβの引き算側の定理をシミュレーターで確認します。

加法定理(引き算)

$ \displaystyle cos(α – β) = cosαcosβ + sinαsinβ$
$ \displaystyle sin(α – β) = sinαcosβ – cosαsinβ $
$ \displaystyle tan(α – β) = \frac{tanα – tanβ}{1 + tanαtanβ} $

シミュレーターの説明

↓でαとβの角度を指定すると「α – β」を加法定理から計算します
αを赤色、βを青色、そして「α – β」の角度領域を緑色で角度表示します
加法定理の計算結果が成り立つことを確認しましょう(小数点2桁表示しているため、微小の誤差はあります)
tan90,270は本来計算できないのですが、ここでは∞としてとりあえず算出しています

角度α

角度β

[結果]
cos()==0.0

sin()==0.0

tan()==0.0

加法定理(足し算)シミュレーター

次はαとβの足し算側の計算を確認してみましょう！

加法定理(足し算)

$ \displaystyle cos(α + β) = cosαcosβ – sinαsinβ $
$ \displaystyle sin(α + β) = sinαcosβ + cosαsinβ $
$\displaystyle tan(α + β) = \frac{tanα + tanβ}{1 – tanαtanβ}$

シミュレーターの説明