「関数の平行移動」をシミュレーション/図解で理解！上下左右に移動させてみよう！[数学入門]

2020-04-10　

関数

1 関数はどうやれば平行移動できるか考えていこう！
2 関数の縦方向(y軸)移動は関数に定数を足すだけ
- 2.1 関数移動シミュレーターで実験！
3 関数の横方向(x軸)移動
- 3.1 関数移動シミュレーターで実験！
4 縦方向・横方向の移動を組み合わせれば、自由に関数を並行移動できる！
- 4.1 関数移動シミュレーターで実験！

関数はどうやれば平行移動できるか考えていこう！

前回の記事で、数学でいう関数とは何かを説明しました。関数とは簡単にいうと、以下のようにxをインプットにし、アウトプットyを何らかの計算で出すものです。

　
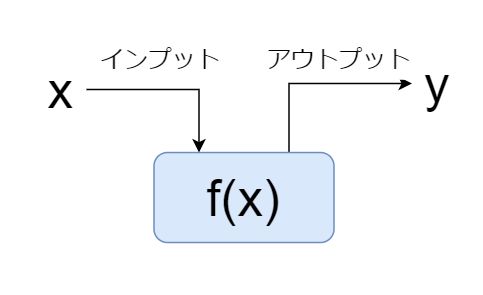
この関数f(x)、中身は色々なものがありますが、、、、一律的な操作で自由に上下左右に移動させることが可能なんです！どのようにすれば、関数f(x)を移動できるのか、、、その方法をシミュレーターを用いて詳しく説明していきます！

関数の縦方向(y軸)移動は関数に定数を足すだけ

まず関数の縦方向の移動について考えます。これは簡単です。どんな関数f(x)であれ、移動したい数Cを足せばよいだけです。上方向に5移動したければf(x)に+5をすれば良いし、逆に下方向に4移動したければf(x)に-4を足せばよいだけです。

つまり、任意の関数f(x)をy軸方向に＋C移動させた関数f'(x)は

関数f(x)をCだけ縦移動

$$ \large{f'(x) = f(x) + C }$$

と表現できます。f(x)にCを足せば良いだけです。Cがプラスであれば、上方向に、マイナスであれば下方向に移動します！

関数移動シミュレーターで実験！

それでは理解を深めるために具体的な関数

$$ \large{y = f(x) = x^3 + 3x -x}$$

をシミュレーターで実際に縦方向に移動してみましょう！

0.0

[関数]
$ {y=} $ $ {x^3 + 3x^2 -x } $ + 0

このように、縦方向の移動は、移動したい分を関数に追加すれば良いだけです。簡単ですね！
　

POINT縦方向の移動は、単純に移動したい数値Cを関数に足せば良い！

関数の横方向(x軸)移動

次に横方向の関数の移動について考えてみます。コチラは少し工夫が必要です。

今、具体例として

$$ \large{y = f(x) = x^3 + 3x^2 -x }$$

という関数と、

$$ \large{y = f'(x) = (x-2)^3 + 3(x-2)^2 -(x-2) }$$

という関数を比較して考えてみます。f'(x)はf(x)のx部分を(x-2)に置き換えたものです。この対応関係を考えてみると、、、

$$ \small{ f'(0) = (-2)^3 + 3(-2)^2 -(-2) = f(-2) } $$ $$ \small{ f'(1) = (-1)^3 + 3(-1)^2 -(-1) = f(-1) } $$ $$ \small{ f'(2) = (0)^3 + 3(-0)^2 -(0) = f(0) } $$ $$ \small{ f'(3) = (+1)^3 + 3(+1)^2 -(+1) = f(+1) } $$

というような関係性になります。コレを見ると、

$$ \large{ f'(x+2) = f(x) } $$

という関係性になっているのが分かりますね。つまり、f'(x)はf(x)を2だけ右に移動した関数と言えます。

図示すると、青線のf'(x)のほうが+2だけ右に移動しているのが分かりますよね。

これはどんな関数でも成り立ちます。f(x)があったときに、そのx要素を(x-B)に置き換えた関数f'(x)は、関数f(x)をBだけ右に移動したものになります。

関数f(x)を横にB移動

$$ \large{f'(x) = f(x-B) }$$

x=Bのとき、f'(B)=f(B-B)=f(0)となる事からも分かると思います。

関数移動シミュレーターで実験！

それでは実際にシミュレーターで動かして見ましょう！以下の例では元の関数

移動前の関数

$$ \large{y = f(x) = x^3 + 3x -x}$$

に対して、xを(x-B)に入れ替え、Bを変化させて実際の横移動を確かめる事ができます！

0.0

[関数]
$ {y=} $ (x + 0)$ {^3 }$ + 3(x + 0)$ {^2 } $ – (x + 0)

POINT横方向の移動は、関数内のxを(x-B)に入れ替えれば良い！

縦方向・横方向の移動を組み合わせれば、自由に関数を並行移動できる！

さて、上記の説明の通り、1)関数に値Cを足し算する縦移動、2)xを(x-B)に置き換える横移動が可能です。

これを組み合わせると、任意の関数f(x)は以下の操作で横にB,縦にC移動することが可能と言えます。

関数f(x)を横にB、縦にC移動

$$ \large{f'(x) = f(x-B) + C }$$

最後に実際に↓のシミュレーターで上下に移動してみて、理解を深めましょう！

関数移動シミュレーターで実験！

以下の例では元関数

移動前の関数

$$ \large{y = f(x) = x^3 + 3x -x}$$

に対して、横移動Bと縦移動Cを変化させて実際の上下の移動を確かめる事ができます！

0.0

[関数]
$ {y=} $ (x + 0)$ {^3 }$ + 3(x + 0)$ {^2 } $ – (x + 0) + 0

このように任意の関数は上記の操作で移動可能です！
　

まとめ

縦方向の移動は、単純に移動したい数値Cを関数に足せば良い
横方向の移動は、関数内のxを(x-B)に入れ替えれば良い

[関連記事] 数学入門：関数

3．関数の平行移動(本記事)

⇒「関数」カテゴリ記事一覧

その他関連カテゴリ

学問系TOP AI/ChatGPT 数学物理統計学コンピューター経済学 Webツール