「ベクトルの内積」をシミュレーション/図解で理解しよう！[数学入門]

2021-02-28　

ベクトル

前回まで基本的なベクトル演算についてお話してきました。
今回は「単位ベクトルの内積」についての解説です。少し難しいですが、ベクトル分野の中で重要なポイントになります。シミュレーターを使ってその意味を理解しましょう！

1 ベクトルの内積の定義
2 ベクトル内積の図形的意味
3 ベクトル内積の成分による計算
- 3.1 上記式の証明
- 3.2 3次元以降も同様に成分表示で内積計算できます！
4 内積の2つの表現からcosθが求められる！
5 シミュレーションでベクトル内積を理解しよう！
- 5.1 2次元ベクトルシミュレーター
- 5.2 3次元ベクトルシミュレーター
6 重要：ベクトル内積の値が0＝なす角が垂直
7 まとめ：内積を使うと2ベクトルの角度を計算出来る！

ベクトルの内積の定義

まずベクトル内積の定義から示します。

ベクトル内積の定義

\( \vec{a}と\vec{b}の内積 \)
\( \displaystyle = \vec{a} \cdot \vec{b} \)
\( \displaystyle = |\vec{a}||\vec{b}|cos\theta \)
* θは\(\vec{a}と\vec{b}\)がなす角の角度

これがベクトル内積です。2つのベクトルにより内積が定義されるワケですね！2つのベクトル(線)があれば、必ずその2つがなす角θが決まります(ゼロベクトル除く)。そのθを使うと、上記のような内積が定義できるワケです。

ベクトル内積の図形的意味

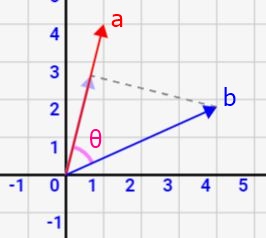
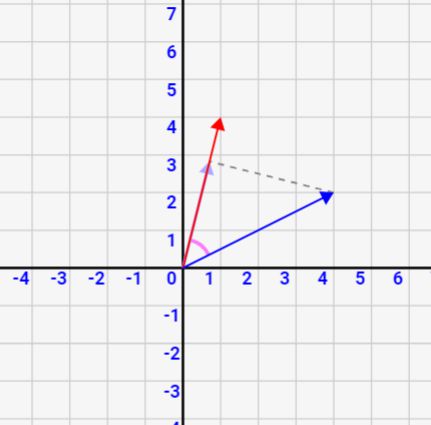
内積の意味を考えると、↓図のような意味と捉えることが出来ます。\(\vec{a}\)を赤矢印、\(\vec{b}\)を青矢印と考えて下さい。2つのベクトルがなす角がθです。

とすると、\(|\vec{b}|\)cosθを「青矢印から赤矢印に、直角に線を下ろした時の長さ」と考える事ができます。cosθは直角三角形において「角θをなす横線と斜辺との比率」です(詳細は三角関数の解説ページ参照)。

ですので、斜辺の長さである\(|\vec{b}|\)にcosθを乗算すると↑図の紫矢印の長さになるワケです。青矢印\(\vec{b}\)から赤矢印\(\vec{a}\)に直角に下ろした時の長さですね。

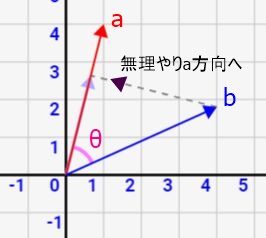
つまり、内積とは「ベクトル\(\vec{a}\)の大きさ」と「ベクトル\(\vec{b}\)を無理やり\(\vec{a}\)方向に下ろした時の大きさ」を掛け合わせた値とも見なせます。

ベクトルはそれぞれ違う方向を向いていますが、↓のように無理やり同じ方向に向けて掛け合わせたのが内積なのです！

ベクトル内積の成分による計算

上記で定義を示した内積ですが、↓のような形でベクトル成分から実は求められます。

ベクトル内積の成分計算(2次元)

\( \vec{a}=(a_1,a_2)と\vec{b}=(b_1,b_2)の内積 \)
\( \displaystyle = \vec{a} \cdot \vec{b} \)
\( \displaystyle = a_1 b_1 + a_2 b_2 \)

この定義であれば、角θがわからなくても内積を計算することが可能なんです！すごく重要なとこです！

上記式の証明

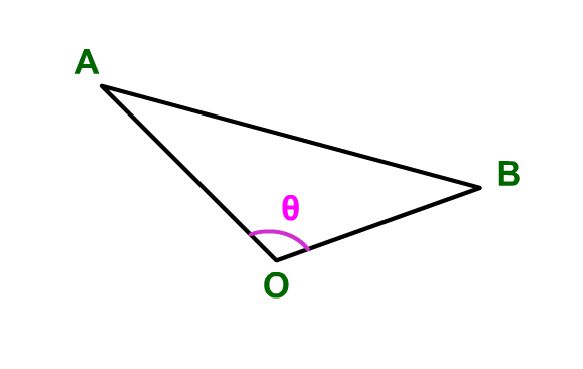
上記式が成り立つことは↓の余弦定理を使うと証明できます（この定理については別ページで解説予定）

前提：余弦定理

\( \displaystyle |AB|^2 = |OA|^2 ＋ |OB|^2 – 2|OA||OB|cos\theta \)

この定理は↓辺ABの長さをその他二辺OA,OBの長さとその二辺のなす角度θから求める公式です。

この余弦定理のOを原点(0,0)とすると、角辺の長さはベクトル形式では↓のように表すことができます。ABはベクトル\(\vec{AO}\)(つまり\(\vec{OA}\)の逆ベクトル)と\(\vec{OB}\)の足し合わせと考えることが出来るからです。

\( \displaystyle OA = \vec{a} \)
\( \displaystyle OB = \vec{b} \)
\( \displaystyle AB = (\vec{b} – \vec{a})\)

上記式にこれを代入すると、↓というように変形できます。

\( \displaystyle |\vec{b} – \vec{a}|^2 = |\vec{a}|^2 ＋ |\vec{b}|^2 – 2|\vec{a}||\vec{b}|cos\theta \)

このとき\(|\vec{a}||\vec{b}|cos\theta\)は内積\( \vec{a} \cdot \vec{b} \)の定義そのものですので、

\( \displaystyle |\vec{b} – \vec{a}|^2 = |\vec{a}|^2 ＋ |\vec{b}|^2 – 2(\vec{a} \cdot \vec{b}) \)
↓変形
\( \displaystyle \vec{a} \cdot \vec{b} = \frac{1}{2}(|\vec{a}|^2 ＋ |\vec{b}|^2 – |\vec{b} – \vec{a}|^2) \)

と表すことができます。これをベクトル成分\(\vec{a}=(a_1,a_2)と\vec{b}=(b_1,b_2)\)を代入していくと、、

\( \displaystyle \vec{a} \cdot \vec{b} \)
\( \displaystyle = \frac{1}{2}((a_1^2 + a_2^2) + (b_1^2 + b_2^2) – ((b_1 – a_1)^2 + (b_2 – a_2)^2 ) \)
↓\(a_1^2, a_2^2, b_1^2, b_2^2\)は打ち消し合い消える
\( \displaystyle = \frac{1}{2}(2 a_1 b_1 + 2 a_2 b_2) \)
\( \displaystyle = a_1 b_1 + a_2 b_2 \)

となり、最終的に

ベクトル内積による等号関係

\( \displaystyle \vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 = |\vec{a}||\vec{b}|cos\theta \)

が言えるわけです！

3次元以降も同様に成分表示で内積計算できます！

上記の2次元の場合と同様に、3次元以降の場合も内積が定義可能です。

ベクトル内積の成分計算(3次元)

\( \vec{a}=(a_1,a_2,a_3)と\vec{b}=(b_1,b_2,b_3)の内積 \)
\( \displaystyle = \vec{a} \cdot \vec{b} \)
\( \displaystyle = a_1 b_1 + a_2 b_2 + a_3 b_3 \)

となります。各成分を乗算して足せば内積になるんですね。

内積の2つの表現からcosθが求められる！

上記のベクトル内積の等号関係は物凄く意味があります。なぜなら、上記式等号関係式を変形すると

ベクトルのなす角θに関する式

\( \displaystyle cos\theta = \frac{a_1 b_1 + a_2 b_2}{|\vec{a}||\vec{b}|} \)

となり、「\(\vec{a}\)と\(\vec{b}\)の成分さえ分かればそのなす角θのcosが求められる」からです。cosθの値さえわかれば、θも求められます！

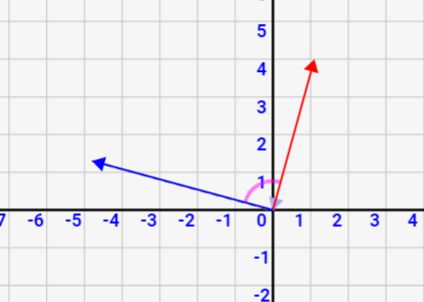
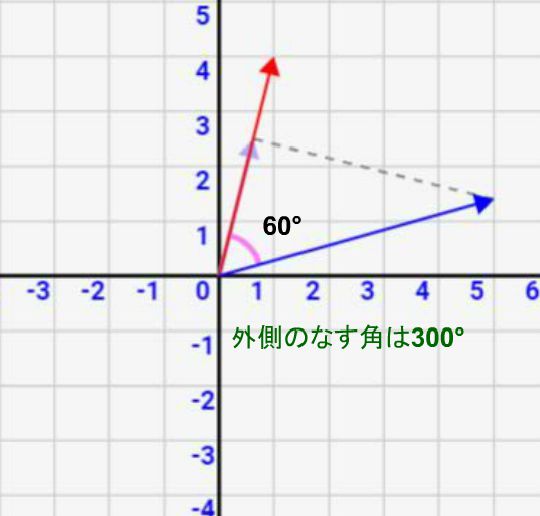
正確にいうと、例えばcosθ=\(\frac{1}{2}\)ならθ=60° or 300°と2パターンの可能性が出てきます。しかしこれは、↓の\(\vec{a}\)と\(\vec{b}\)のなす角が実は内と外2つあるからで、、、そのうち小さい方の内側\(0 \leqq θ \leqq 180\)と条件を定めればθ=60°と一意に求めることができます！
　
↓実は2つのベクトルは内側(60°)と外側(300°)の2つあるが、両方ともcosθ=\(\frac{1}{2}\)

シミュレーションでベクトル内積を理解しよう！

ベクトル内積を求めるシミュレーターを用意しました。元ベクトルの各成分を変えられるので、色んなパターンのベクトル内積の意味を図上で確認してみましょう！

2次元ベクトルシミュレーター

まずは簡単に2次元の例からです！

シミュレーターの説明

\(\vec{a}\)と\(\vec{b}\)のx,y成分を変更すると、それに従って計算結果が表示されます
内積だけでなく、そこから求めたcosθとθ角度も計算出力します
紫矢印で\(\vec{b}\)を\(\vec{a}\)に垂直に下ろした長さも表しています

色々値を変えてみて、それをもとに内積の意味を理解しましょう！

\(\vec{a}\)成分(赤矢印)

1.0

4.0

\(\vec{b}\)成分(青矢印)

4.0

2.0

\(\boldsymbol{a} \cdot \boldsymbol{b}\)=
\( cosθ \)=
\( θ \)=°

3次元ベクトルシミュレーター

次に3次元のパターンです。内積は3次元でも定義可能なことを、このシミュレーターを用いて理解しましょう！

シミュレーターの説明

\(\vec{a}\)と\(\vec{b}\)のx,y,z成分を変更すると、それに従って計算結果が表示されます
内積だけでなく、そこから求めたcosθとθ角度も計算出力します
紫矢印で\(\vec{b}\)を\(\vec{a}\)に垂直に下ろした長さも表しています

\(\vec{a}\)成分(赤矢印)

1.0

4.0

\(\vec{b}\)成分(青矢印)

4.0

2.0

\(\boldsymbol{a} \cdot \boldsymbol{b}\)=
\( cosθ \)=
\( θ \)=°

重要：ベクトル内積の値が0＝なす角が垂直

ベクトル内積が0の場合を考えると、以下のような関係式が成り立ちます。

ベクトル内積0の場合

\(\vec{a}≠0\),\(\vec{b}≠0\)でないならば
\(\boldsymbol{a} \cdot \boldsymbol{b} = 0 \Leftrightarrow \vec{a}
\perp \vec{b} (\vec{a}と\vec{b}が垂直) \)

これは内積の定義が\(|\vec{a}||\vec{b}|cos\theta\)であり、\(\vec{a}≠0\),\(\vec{b}≠0\)という条件下で\(cosθ=0\)となることが必須となるからです。そうなるのはθ=90° or 270°の時のみであり、つまり\(\vec{a},\vec{b}\)が直角と言えるわけです。

この関係性は、上で説明した内積とは「ベクトル\(\vec{a}\)の大きさ」と「ベクトル\(\vec{b}\)を無理やり\(\vec{a}\)方向に下ろした時の大きさ」を掛け合わせた値という意味から考えても自明です。ベクトルが垂直であれば「ベクトル\(\vec{b}\)を無理やり\(\vec{a}\)方向に下ろした時の大きさ」は0になるので、内積0になるのは当然です。