「ベクトルの足し算・引き算」をシミュレーション/図解で理解しよう！[数学入門]

2020-12-07　

ベクトル

本ページでは数学のベクトルの基礎について、シミュレーターを用いてその意味・定義について解説しています。

今回は「ベクトルの足し算・引き算」についての解説です。ベクトルは向きがあるので、通常の数値の足し算とは少し違います。その辺りについて、詳しく解説します！

1 ベクトルの足し算を定義
2 ベクトルの足し算の図形的意味
3 ベクトルの引き算は「逆ベクトルとの足し算」
4 シミュレーションでベクトルの足し算/引き算を理解しよう！
- 4.1 2次元ベクトルシミュレーター
- 4.2 3次元ベクトルシミュレーター
5 ベクトルの足し算・引き算の要点
- 5.1 要点1：一般的に「ベクトルaの大きさ + ベクトルbの大きさ＝ベクトルa+bの大きさ」は成り立たない！
- 5.2 要点2：ベクトルの引き算結果は、2つのベクトル間を結んだベクトル
6 まとめ：ベクトルの足し算は、2つの矢印を合成すること！

ベクトルの足し算を定義

ベクトルの足し算は以下のように定義できます。

ベクトルの足し算の定義(2次元)

\( \vec{a} = (x_a,y_a) \)
\( \vec{b} = (x_b,y_b) \)
とした時、
\( \vec{a} + \vec{b} \)
\( \displaystyle = (x_a,y_a) + (x_b,y_b) \)
\( \displaystyle = (x_a + x_b, y_a + y_b) \)

つまり、単純に成分ごとに足し算をすればいいんです。

3次元の場合も同様で

ベクトルの足し算の定義(3次元)

\( \vec{a} = (x_a,y_a,z_a) \)
\( \vec{b} = (x_b,y_b,z_b) \)
とした時、
\( \vec{a} + \vec{b} \)
\( \displaystyle = (x_a,y_a,z_a) + (x_b,y_b,z_b) \)
\( \displaystyle = (x_a + x_b, y_a + y_b, z_a + z_b) \)

となります。

ベクトルの足し算の図形的意味

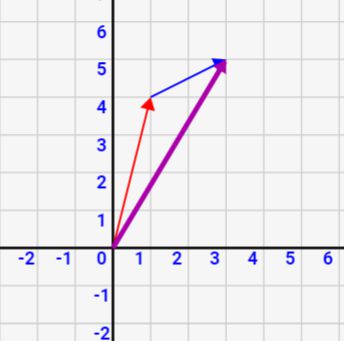
上記の通りベクトルの足し算を定義しますが、図にするともっと分かりやすいです。ベクトルの足し算は、「ベクトル\(\vec{a}\)の先にベクトル\(\vec{b}\)を結合したベクトル」になります。

↓がその図です。赤矢印が\(\vec{a}\)、青矢印が\(\vec{b}\)、そして足したベクトルが紫矢印です。赤矢印と青矢印を結合したものが、紫矢印と同一になっていますよね。ベクトルの足し算はこのように、2つのベクトルを結合するイメージで捉えれば簡単です！

ベクトルの引き算は「逆ベクトルとの足し算」

続いてベクトルの引き算の説明です。二次元での定義は↓の通りです。

ベクトルの引き算の定義(2次元)

\( \vec{a} = (x_a,y_a) \)
\( \vec{b} = (x_b,y_b) \)
とした時、
\( \vec{a} – \vec{b} \)
\( \displaystyle = (x_a,y_a) – (x_b,y_b) \)
\( \displaystyle = (x_a,y_a) + (-x_b,-y_b) \)
\( \displaystyle = (x_a – x_b, x_b – y_b) \)

3次元の場合は省略しますが、同様の式になります。つまり、成分同士の引き算をすればいいことになります。このとき実は「\(\vec{b}\)の逆ベクトルを足している」と考えることもできます。途中で出てくる「\((-x_b,-y_b)\)」はまさに\(\vec{b}\)の逆ベクトルですから。

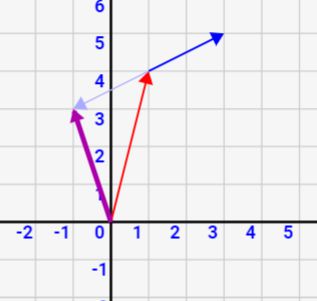
すると引き算も↓のように簡単に図示できます。薄青矢印が\(\vec{b}\)の逆ベクトルです。足し算との違いは、「\(\vec{b}\)を反対にしてから結合する」という事だけです！

シミュレーションでベクトルの足し算/引き算を理解しよう！

ベクトルの足し算/引き算ができるシミュレーターを用意しました！ベクトル\(\vec{a}\)と\(\vec{b}\)の各成分を変えられるので、色んなパターンの足し算/引き算を実験してみましょう！

シミュレーター上は\(\vec{a}\)を赤矢印、\(\vec{b}\)を青矢印、足し算/引き算の結果を紫矢印で表現しています！
引き算の場合は、\(\vec{b}\)の逆ベクトルを薄青矢印で表現して、分かりやすいようにしています！

2次元ベクトルシミュレーター

まずは簡単に2次元の例からです！

シミュレーターの説明

\(\vec{a}\)と\(\vec{b}\)のx,y成分を変更すると、それに従って計算結果が表示されます
演算方式「足し算」「引き算」を選択できます。その違いを確かめてみて下さい

色々値を変えて、足し算・引き算のイメージを掴んでみて下さい！

\(\vec{a}\)成分(赤矢印)

1.0

4.0

\(\vec{b}\)成分(青矢印)

2.0

1.0

演算

足し算引き算
　

3次元ベクトルシミュレーター

次に3次元の場合です！

シミュレーターの説明

\(\vec{a}\)と\(\vec{b}\)のx,y,z成分を変更すると、それに従って計算結果が表示されます
演算方式「足し算」「引き算」を選択できます。その違いを確かめてみて下さい

色々値を変えて、足し算・引き算のイメージを掴んでみて下さい！

\(\vec{a}\)成分(赤矢印)

1.0

4.0

2.0

\(\vec{b}\)成分(青矢印)

2.0

1.0

3.0

演算

足し算引き算
　

ベクトルの足し算・引き算の要点

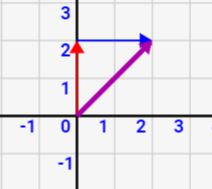
要点1：一般的に「ベクトルaの大きさ + ベクトルbの大きさ＝ベクトルa+bの大きさ」は成り立たない！

最後に補足です。ベクトルの足し算により、ベクトルの大きさは合成されます。しかし、単純な「ベクトルaの大きさ + ベクトルbの大きさ＝ベクトルa+bの大きさ」は一般的に成り立ちません。

↓図で考えるとそれが明白です。ベクトル\(\vec{a}\)とベクトル\(\vec{b}\)はともに大きさ2です。しかし、足した斜めベクトルの大きさは明らかに4ではないですよね。斜めの長さなので、明らかに4より小さいはず。

これはベクトルがともに違う方向を向いているからです。ベクトルは向きがあるので、このように大きさが単純な加算ではなくなります。ご注意を！

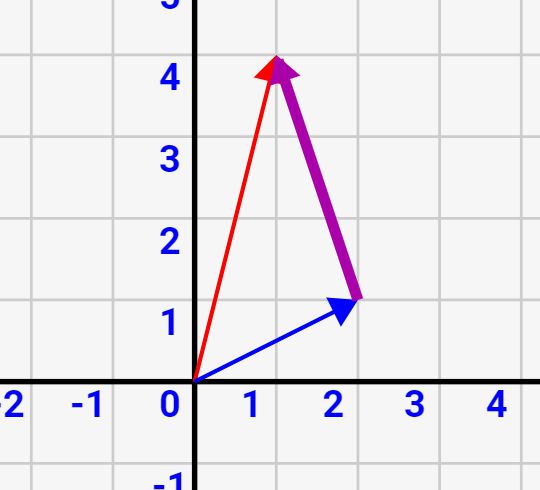
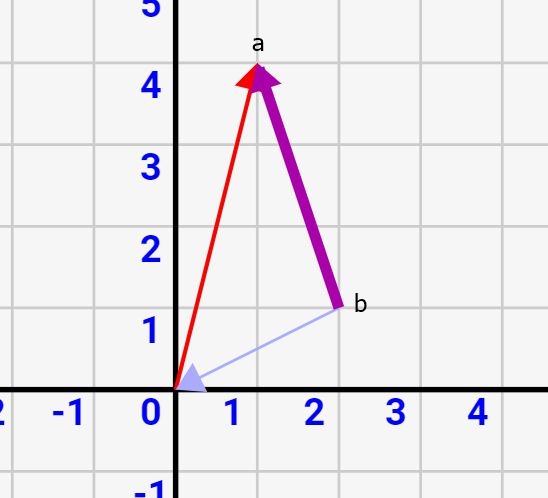
要点2：ベクトルの引き算結果は、2つのベクトル間を結んだベクトル

上記ではベクトルの引き算は、「\(\vec{a}\)から\(\vec{b}\)の逆ベクトルを足す演算」と説明しました。しかし、ベクトル引き算にはもう一つの意味合いがあります。それは、「引き算結果は\(\vec{b}\)をスタート地点、\(\vec{a}\)をゴール地点として結んだベクトルになる」というものです。つまり↓図の紫ベクトルになります。