「ベクトルの大きさ変更(実数倍)」「逆ベクトル・零ベクトル」をシミュレーション/図解で理解しよう![数学入門]
今回は「ベクトルの大きさ変更(実数倍)」と「逆ベクトル・零ベクトル」について説明していきます。ベクトルには「方向」「大きさ」の2つの性質がありますが、そのうち今回は「大きさ」について、どのように変わるのか説明していきます!逆ベクトル・零ベクトルはその操作から自然と出てくる概念です!
![「ベクトルの大きさ変更(実数倍)」「逆ベクトル・零ベクトル」をシミュレーション/図解で理解しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20210228170956.jpg)
目次
ベクトルの拡大・縮小(実数倍)
前回記事のようにベクトルには大きさがあります。今回はその大きさに着目し、ベクトルを拡大・縮小(実数倍)することを考えます。
ベクトルを拡大縮小するときには、実数を乗算します。例えば、ベクトル\(\vec{a}\)をk倍したベクトルを\(\ k \vec{a}\)と表現します。2倍なら\(\ 2 \vec{a}\)と書くということです!
実際の成分ごとに見た、実数k倍することの定義は以下の通りになります。
\( ベクトル\vec{a}(x,y,z)のk倍 \)
\(\ \displaystyle = k \vec{a}\)
\( \displaystyle = (kx,ky,kz) \)
つまり、ベクトル\(\ \vec{a}\)をk倍するとは、その各成分(x,y,z)それぞれk倍にして、(kx,ky,kz)とすることになります!全ての要素を同じだけk倍引き伸ばすので、向きは変わらず、大きさだけが変わるわけです!
ただ、kの値によってどのようなベクトルになるかが以下のように変わってきます。
[k > 0の場合]
ベクトル\(\vec{a}\)と同じ向きで、大きさが\(|k|\)倍のベクトルとなる
[k < 0の場合]
ベクトル\(\vec{a}\)と真逆で、大きさが\(|k|\)倍のベクトルとなる
[k = 0の場合]
零ベクトルになる(後述)
k=0の場合は後述するので今は無視して下さい。重要なのは「kが正の数か負の数かによって、向きが真逆になる」ということです。大きさは\(|k|\)倍になるのは同じですが、負の数の場合は向きが逆になります。
シミュレーターでベクトルの実数倍のイメージをつけよう!
ベクトルを実数k倍することを学びましたので、実際にシミュレーターで確かめてみましょう!
2次元ベクトル シミュレーター
まずは簡単に2次元の例からです!
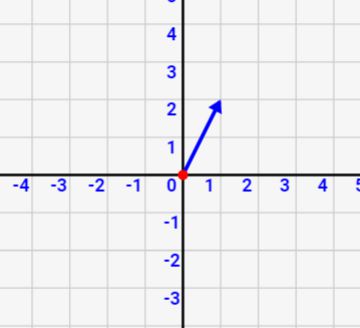
- 簡単のために元ベクトルは\(\vec{a}=(1,2)\)に固定しています
- スライドバーで乗算するkが変えられます
- 元ベクトルは青矢印で、k倍したベクトルを赤矢印で表示しています
kを色々変更してみて、赤矢印がどう変わるか実験してみて下さい!
向きが変わらず、大きさだけが変わるのが重要ポイントです!また、kを0にしたり、負の数にしてみてどう変わるかも確認してみて下さい!
3次元ベクトル シミュレーター
次に3次元の例です!
- 簡単のために元ベクトルは\(\vec{a}=(1,2,1)\)に固定しています
- スライドバーで乗算するkが変えられます
- 元ベクトルは青矢印で、k倍したベクトルを赤矢印で表示しています
2次元の場合と同様に乗数kを変えてみて、赤矢印の大きさが変わる様子を確認しましょう!
逆ベクトル=逆向きの矢印
ベクトルには重要な概念として「逆ベクトル」というものがあります。その定義は以下の通りです。
ベクトル\(\vec{a}\)と反対向きで、ベクトル\(\vec{a}\)と長さが同じベクトル
簡単にいうと「ベクトル\(\vec{a}\)の反対」です。絵にすると↓になります。反対方向向いていますよね。これを\( – \vec{a}\)と記号で表現します。
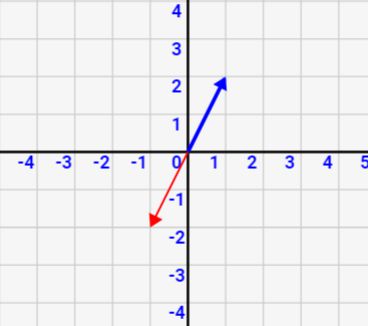
この逆ベクトル、成分表示で正式に定義すると以下のようになります。
\( ベクトル(x,y)の逆ベクトル \)
\( \displaystyle = (-x,-y) \)
つまり、逆ベクトルはベクトル\(\vec{a}\)を-1倍したものになります。ですので、上のシミュレーターでk=-1を入力したときに相当します!そのとき真逆のベクトルになるため、「逆ベクトル」という名前がついているわけです!
零ベクトル=大きさ0のベクトル
次に重要な概念として、「零ベクトル」があります。この定義は以下の通りです。
大きさが0のベクトル
ただの点です。ですので全ての要素が0となります。二次元ベクトルの例で表すと以下のようになります。
\( 零ベクトル \)
\( \displaystyle = (0,0) \)
このように特殊な形であるため、以下のような特殊な性質を持ちます。
大きさ0のため、向きを持たない
普通のベクトルは必ず向きを持ちますが、零ベクトルだけは点になるため向きがないのです。特殊なベクトルなので、注意して扱う必要があります!
k=0を乗算すると、どんなベクトルも零ベクトルになる
どんなベクトルでもk=0を乗算すれば零ベクトルになります。全ての成分に0をかけるので当然ですね。↑のシミュレーターでも、k=0にすると↓の図のようになり、ベクトルでなくただの点(零ベクトル)になります。
\( \displaystyle = (0*x,0*y) \)
\( \displaystyle = (0,0) \)
補足:ベクトルと逆ベクトルを足すと、零ベクトルになる
ベクトルの足し算は次回以降で説明しますが、先に説明を。どんなベクトルでも、逆ベクトルを足せば↓のように零ベクトルになります。
\( \displaystyle = (x,y) + (-x,-y) \)
\( \displaystyle = (0,0) \)
反対の向きなので打ち消し合うわけですね!
まとめ:ベクトルに実数をかけると拡大縮小される。-1倍すると逆ベクトル、0倍すると零ベクトルになる!
最後にまとめです。ベクトルは実数をかけて拡大・縮小することができます。k倍することで大きくしたり、小さくしたりできます。負の数をかけると逆向きになることに注意です。
逆ベクトルという概念も重要です。これは、-1倍かけたベクトルであり、もとのベクトルの真逆のベクトルとなります。
また、0倍すると零ベクトルになります。零ベクトルは成分0のベクトルで、向きを持たないという特殊なベクトルになります。ただの点ですね。扱いには注意が必要です!
次回は単位ベクトルについて解説していきます!
⇒「ベクトル」カテゴリ記事一覧
その他関連カテゴリ