「小規模集団での統計調査、何%調べれば良いか?」その疑問をシミュレーターで理解しよう!一人の経験則なんてあてにならない!
前回は「視聴率」という、全体が1億世帯レベルの大きな場合のサンプル数の取り方の話をしました。
今回は、もっと小規模の団体での話です。例えば1000人の会社内とか、100人の同学年集団とか。そういった集団で、ある程度の傾向を調べるために「何人ぐらい調査すれば良いか」をシミュレーターで直感的に分かるようにしてみました!
目次
「統計調査」は、いろんな場面で用いられます!
統計調査とは
前回は「視聴率」についての大規模な統計調査について考察しました。そもそも統計調査とは何かというと、、、↓のようなものが例として挙げられます。
会社全体でiPhone/Androidを持っている率
市内で運転免許を持っている人の率
学年全体で体重が〇以上の人の率
区内での自転車所持率
学校全体で校則変更に賛成/反対の人の率
クラス内の性格が悪い人の率
こういった調査は、もちろんその集団全員を調査すれば良いのですが、、、ただ「100人のうち50人調査」とかでもある程度傾向がわかりそうですよね!
今回はその「〇人の集団のうち、〇人調べたらどの程度の誤差がでてくるか」を直感的にグラフで分かるようにしました!1000人以下とか、ある程度小規模の集団に絞ってます。
母集団人数による、推定グラフのバラツキ方の違い
前回記事でも書いた通り「日本人全体」という1億レベルの調査であれば、大概の調査は「数千人規模調査で1,2%誤差レベルの傾向がわかる」という事になります。トリビアの泉で、毎回統計の先生が「2000人調査すれば良い」といってましたが、そんな感じなんです。
しかし、小規模団体の場合は、そのその集団(母集団といいます)の数によって、バラツキ方が大きく変わります。100人サンプル調査でも、「母集団が100人しかいない場合」「母集団が10000人いる場合」で全く意味合いが異なってます。
条件:無作為抽出前提
今回のシミュレーターは当たり前ですが、「無作為抽出」前提です。無作為とはランダムに人やモノを選ぶという意味です。調査が楽だから、市内の調査だけど近くに住んでる人を選ぶ、、、とか変なことすると調査が偏ってしまうので絶対にダメなんですね><
「統計調査の推定値バラツキ」シミュレーター
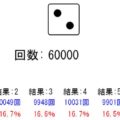
- 今回は統計調査をクジ引きと置き換えて、シミュレートします。「当たり=調査してる対象に合致」という意味です(↑の例でいうとiPhone持ってる、自転車持っている等)
- 今回は総数(母集団)とサンプル数と真の当たり率を指定すると、それに従って推定の当たり率がどれぐらいバラつくかをシミュレートして表示します
- 「サンプル数>総数」はあり得ないので、その場合は「サンプル数=総数」とみなしてシミュレートします
- グラフの縮尺は、観察しやすいように自動で調整されるので、注意して下さい
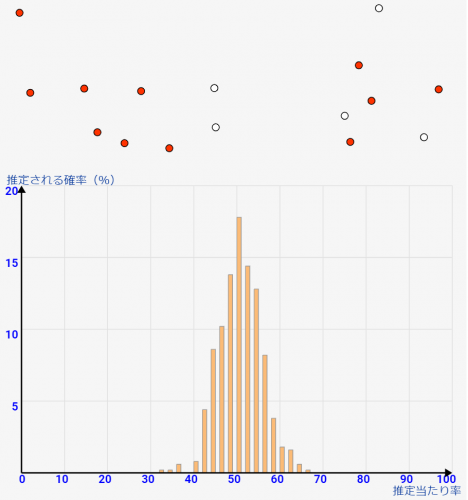
↓図はクジのイメージです。赤が当たりです。
シミュレーター結果考察
やはり、小数だと前回の視聴率調査よりも、バラツキはでてきます。以下当たり率50%固定で見ていきます
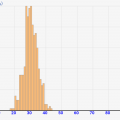
↓[総数100人で50人調査の場合]です。半数の調査ですが、前後8%弱の誤差はでますね。50%のはずが45%とか55%とか判定される可能性も高いということです。逆にこれぐらいの誤差が許容できるのなら、半分の調査で十分なんですね
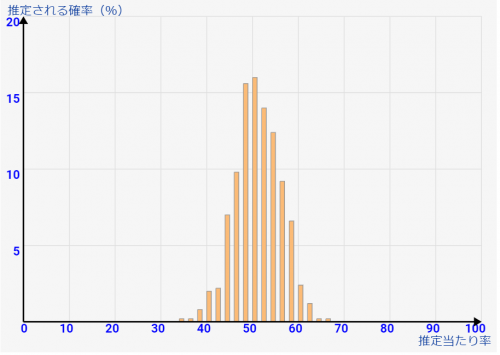
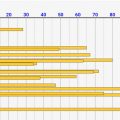
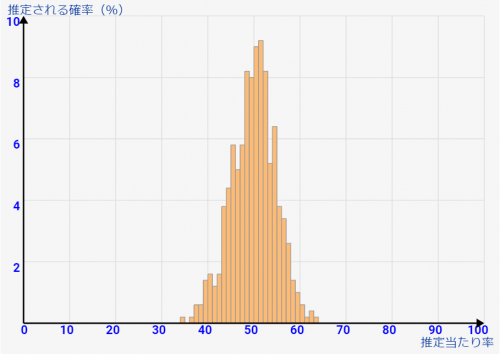
↓[総数1000人で50人調査の場合]です。↑と同じサンプル数ですが、総数が1000人と10倍です。なのでさすがに1/20サンプルということで、バラツキも激しくなっています。
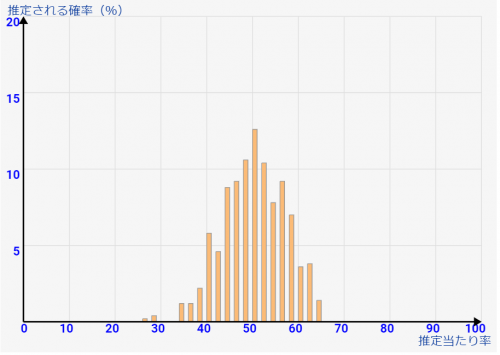
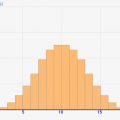
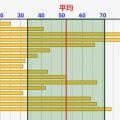
↓[総数1000人で100人調査の場合]です。1/10調査ですが、誤差は8%弱に収まりそうなレベルです。サンプル率は結構低いのですが、これでもある程度は傾向わかりますね。
これを見ていくとわかりますが、「母集団が多いと、サンプル率がある程度低くても誤差は少なくできる」のが分かりますね!逆に言うと、↓のように「総数が少ないと、誤差が大きくなってしまう」んですね>< 小規模集団なら面倒がらずに全部調べろ!ってことなんです。
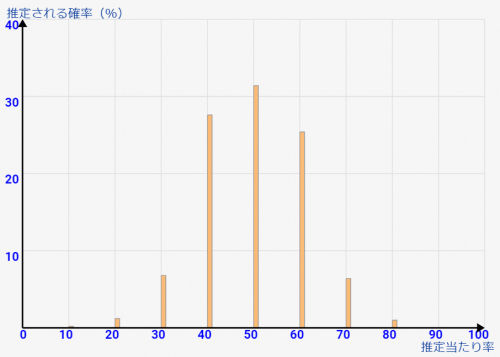
↓[総数20人で10人調査の場合] サンプル率50%ですが、バラつきまくりで20%誤差とかもあり得そうです。
まとめと考察:一人の経験則なんてあてにならない!
今回の考察からわかるのは「一人の経験則なんて、あまりあてにならない」という事です。
例えば、ある50人クラスで、Aさんがクラス10人ぐらいと触れ合った上で「このクラスは自転車持ってる人が多い」「このクラスはiPhone率が高い」「このクラスは性格が悪い人が多い」と判断したとします。
でも、クラスに50人いるなら、↓の[総数50人 10人調査]のサンプリング状態のようになります。これってめちゃくちゃバラついていて信用ならないですよね。
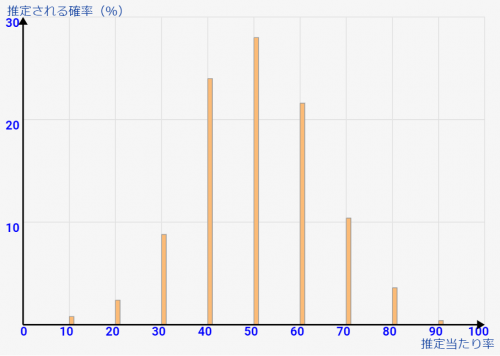
たとえ半数の[総数50人 25人調査]で判断しても↓のような感じ。まだバラツキが広いですね。これはつまり「偶然、確率的に、そのような人と多めに触れ合う事になった可能性が捨てきれないぐらい高い」状態です。
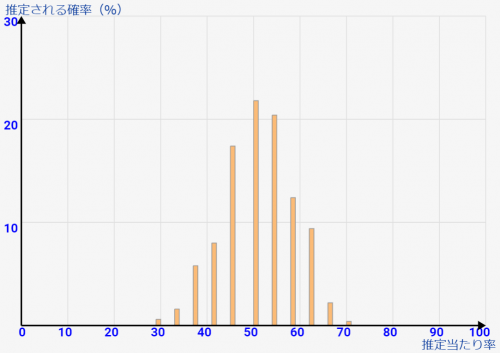
正確に判断するには、50人全員に近いぐらい触れ合って調べないと判断できないんですよね。こう思うと、如何に私達が経験則で不正確に判断しているかが分かります。
正直、クラスの半数と触れ合ってたら「絶対そうだ!」って思ってしまいますもんね。もっというと、2,3人悪い人がいただけで「このクラスは性格悪い!」と思っちゃう人も結構いると思いますし。
ただ、不正確でも、こういった経験的な判断/認識が必要になることもあるので、、、難しいとこですよね><
- 統計
- 母集団数(総数)が大きくなるほど、サンプル率は低くても誤差が低くなる
⇒「サイコロとクジで学ぶ確率統計」カテゴリ記事一覧
その他関連カテゴリ