中央値とは何か?をシミュレーターを用いて詳しく解説!実験で深く理解しよう![統計学/確率入門]
本サイトでは、数学分野の内容を基礎から分かりやすくシミュレーターを用いて解説しています!このベースを用いて、以後「統計学/確率」の分野の内容を同様にシミュレーターを作って解説していきたいと思います!
前回の記事では統計上一番重要な、「平均値」について解説しました。これは統計データの「真ん中」を表す概念でした。
しかし、「真ん中」を表す代表値は平均だけではありません。この記事では別の代表値である「中央値」について解説していきます!
「平均値」と「中央値」の違いがわかるように解説していきます!
![中央値とは何か?をシミュレーターを用いて詳しく解説!実験で深く理解しよう![統計学/確率入門]](https://retu27.com/wp-content/uploads/rapture_20200628212654-500x316.jpg)
目次
「平均値」だけが真ん中とは限らない!データが偏りがあるときに違和感発生!
前回記事で説明した平均値とは
\( \LARGE 平均値 \)
\( \displaystyle = \frac{1}{n}(x_1 + x_2 + … + x_n) \)
\( \displaystyle = \frac{1}{n}\sum_{i=1}^{n}x_i \)
というものでした。つまり、全てのデータ値(\(x_i\))の合計をデータ総数nで割ったものです。ここで一つ問題があります。データ分布に偏りがある場合、平均値が感覚的な「真ん中」とかけ離れる可能性があるんです。
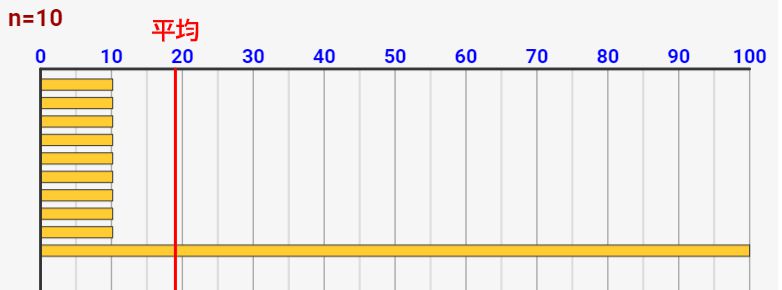
今回も前回記事と同様に0~100点のテストの統計を考えるとします。今、n=10人のテスト結果の分布が以下のようになっているとします。ほとんどの人が10点しかとれず、一人の天才だけ100点をとっている場合です(^^)
このとき平均値の定義から計算すると、平均値は19点になります。しかし、ほとんどの人が10点のテストです。真ん中である平均値は19点、、、9割の人は平均の1/2ぐらいしか点数がとれていないという結果です。
どうでしょうか。感覚と少し違いますよね。これだと多くの人は平均点以下で落第になってしまいそうです><
つまり、「平均値≠普通の人の普通の平均」なんです。そうでなく、どちらかというと、下から並べて「真ん中あたりの人の結果」を用いたいですよね。この考えが「中央値」です。
中央値の定義:下から並べて中間の人の点数をもってくる
上記のような考え方から、中央値を定義を考察していきます。正式な中央値の定義は以下のとおりです。
\( \LARGE 中央値 \)
[データ個数nが奇数の場合]
\( \displaystyle = 下から並べて\frac{n+1}{2}番目(中間)となる点数 \)
[データ個数nが偶数の場合]
\( \displaystyle = 下から並べて\frac{n}{2}と(\frac{n}{2}+1)の結果の平均 \)
です。わかりにくいので例を上げると、
n=11だった場合は、奇数なので下から並べて\(\frac{12}{2}=6\)番目の人の点数
n=10だった場合は、偶数なので下から並べて\(\frac{10}{2}=5\)と\((\frac{10}{2}+1)=6\)番目の人の点数の平均値
となります。つまり、簡単にいうと「とりあえず真ん中の人の結果をもってくる」というのが中央値です。偶数の場合は真ん中が二人になるので、その二人の平均を持ってくるという、それだけの話です!
上記のような偏りは特殊な例ではない!日本の年収の分布でも同様の問題が!
上記のような偏った分布の話を聞いても、「そんな偏ったテスト結果に普通ならないでしょ」と思うかもしれません。でも、こういった偏った分布は多くの世界で頻繁におきます。
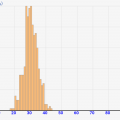
一番わかりやすいのが年収の例です。日本人の年収は平均値が420万円、中央値が360万円程度だそうです。この差は何か。それは、↓のように一部の年収が凄く高い人達によって平均値が一気に押し上げられているからです。ですので、「平均値420万円」だけ見ても、「多くの人が年収420万に達していない、、、」という事が起きるわけです。
こういったときに、真ん中を示す値として「中央値」で見たほうが直感にあっていて良いんですね(^^)
中央値の決まり方をシミュレーターで体感しよう!
「中央値」の具体的なイメージをつけるためにシミュレーターを動かして実験してみましょう!
- スライドバーでn(人数、データ個数)を変えるとシミュレーターが動き出します
- シミュレーターはn人の点数を0~100までランダムで算出して、棒グラフとして点数を描画していきます
- 全て描くと、その後に全ての棒を点数順に並び替え、中央値を上記の定義に基づいて決定して緑線で示します
- 同時に中央のテスト結果をオレンジ色に塗って示します
どのように平均値が動いていくかを確かめましょう!少なくとも、nが奇数の場合と偶数の場合、2パターンは試して見て下さい!
中央値の決まり方
シミュレーション結果をもとに、中央値の決まり方について解説しておきます!
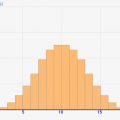
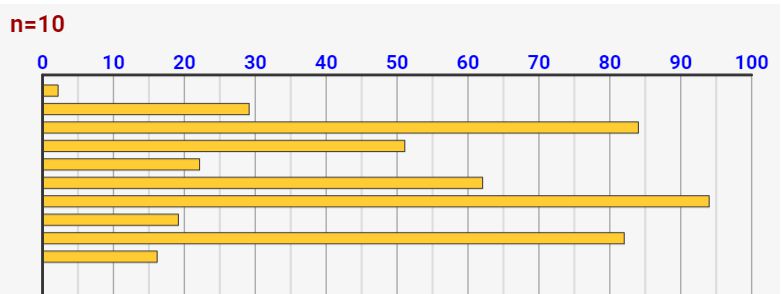
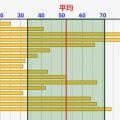
n=10の場合、ランダムにテスト結果が決まっていき、以下のような分布になったとします。
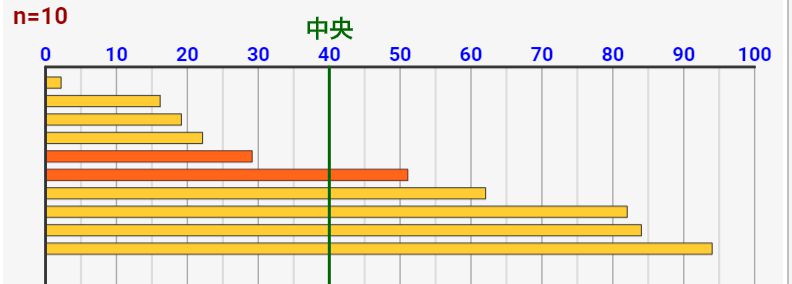
このままだとどれが中央となる結果なのかわからないですね。ですので、テスト結果順で以下のように並び替えをします。
並び替えた結果、中央にきたものが中央値になります。nが偶数の場合、真ん中の結果が2つになるので、その2つの間の値が中央値になります。これが「中央値」の決め方です!
自分でシミュレーターに点数を入力していき、中央値と平均値の動きの違いを理解しよう!
最後におさらいとして、自分で点数を入力し、「中央値」と「平均値」の違いを確かめてみましょう!
- 入力したテスト点数により、平均値(赤線)と中央値(緑線)をリアルタイムに算出して表示します
- 上のシミュレーターと同じく、中央となるテスト点数はオレンジ色で表示します
- スライドバーを動かすと、指/マウスを離した時点でその点数が追加されます
- リセットボタンで初期化できます
スライドバーをポンポンと押しながらデータを追加していき、平均値と中央値の動きの違いを確かめて見ましょう!
基本的に、偏りが少なく均等に分布であれば、平均値と中央値の値はnが増えるほど近い値になっていきます!
次回は「分散/標準偏差」について解説します!
真ん中を示す代表値としては「平均」と「中央値」があります。(その他もあるけど、後に解説予定)
これに対して、統計的な代表値としてはこの「真ん中」を表すもの以外に、「どれぐらいバラついているか」を表すものがあります。これが「分散/標準偏差」であり、平均の次に重要な考え方になります。
次回記事では「バラつきとは一体なんなのか?」という部分を、シミュレータを用いて分かりやすく解説する予定です!
- 平均値は偏りがある場合に、真ん中から大きくハズレる。万能であるわけではない
- 中央値を使うと、真ん中の人の値をピックアップできる
- 真ん中が二人いる場合は、その二人の中間値が中央値となる
⇒「平均/分散等の代表値」カテゴリ記事一覧
その他関連カテゴリ