「視聴率調査ってなんで数千世帯しか調べないの?」その疑問をシミュレーターで解き明かそう!
今回は「視聴率」に関するお話です。昔から視聴率調査は、全世帯数から比べるとかなり少ない数だけで調べられています。
日本全体で6000万世帯ぐらいあるのですが、調査は5000世帯ぐらいしかしないようです。少ないですよね!><
1万分の1ぐらいしか調べてないけど、、、本当に正確なんでしょうか?その謎をシミュレーターで解き明かします!
目次
「視聴率調査」シミュレーターで確かめよう!
さっそく、視聴率調査シミュレーターで「本当に数千世帯の調査で大丈夫なのか?」を調べてみましょう!
シミュレーターの説明
シミュレーターは「指定されたサンプル数」の抽出を繰り返し行い、そこから判定された推定視聴率を分布化してグラフにします。
推定は↓のような一般的な計算方法です。
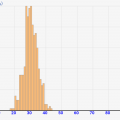
例えば「真の視聴率=30%」でサンプル数が100のときの推定視聴率分布は↓のようになります。グラフの横軸が推定視聴率で、縦軸が「何%の確率でその推定視聴率と判断されるか」です。
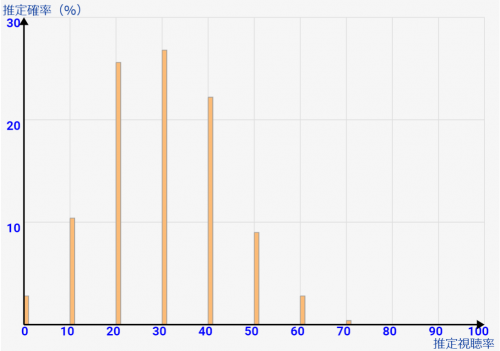
かなり横に広めに分布されます。これは、サンプル数が10と少ないので、偶然7人見ていた人を引いてしまうと、推定視聴率=70%と判定されてしまうためです!かなり不正確ですよね。
推定視聴率は1%ごとでまとめて、↑のように棒グラフで表します(ヒストグラム)。サンプル数が低いときには↑の計算方法により、歯抜け状の棒グラフになります。
「視聴率調査」シミュレーター
- ↑の説明の通り、サンプル数と真の視聴率を指定すると、それに従って推定視聴率の分布を表示します
- ↓のようにサンプル調査の状況をクジのようにして表しています。「視聴していた世帯=赤」「見てなかった世帯=白」として表しています
- 全世帯数=1億と設定しています。ほぼ無限だと思ってください
- グラフの縮尺は、観察しやすいように自動で調整されるので、注意して下さい
シミュレーター結果考察
サンプル数による推定分布の変化
真の視聴率はどの値でも、大きく推定誤差に影響ありません(厳密にいうと、端にいくほど誤差は小さくなりますが)。重要なのは「サンプル数」です。
真の視聴率を30%に固定して、サンプル数を増やしていった状態を見てみます。
[サンプル数=10] とてつもなくバラついていて信用できませんね

[サンプル数=50] まだバラついていて、10%ぐらいの誤差がでてしまいそうです。
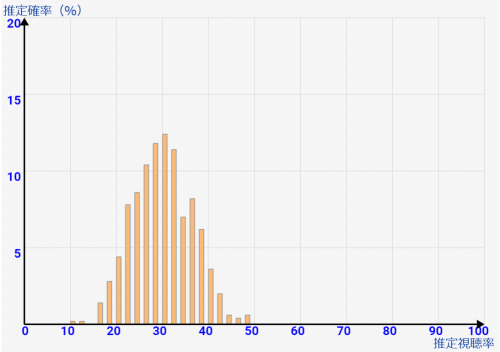
[サンプル数=100] 5%ぐらいの誤差がでてしまいそうな感じです。ある程度の推定はここでもできます。
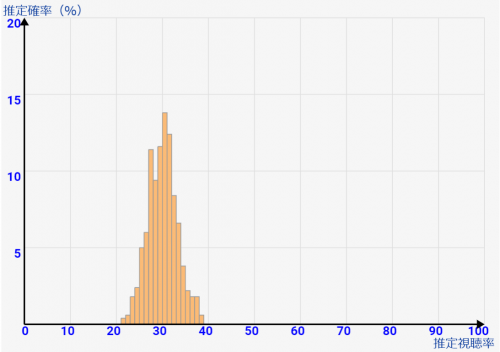
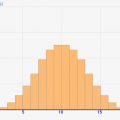
[サンプル数=1000] 3%ぐらいの誤差で納まる範囲になってきています。そこから外れるのはほぼ偶然レベルです。
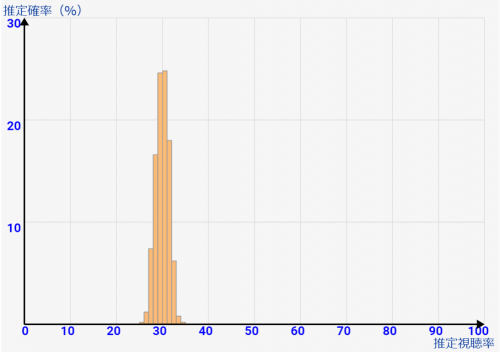
[サンプル数=5000] 全体で4メモリぐらいにおさまってます。ほとんどの場合29~30%と判断され、広くみても28~31%の範囲でほぼ判定されることを意味しています。
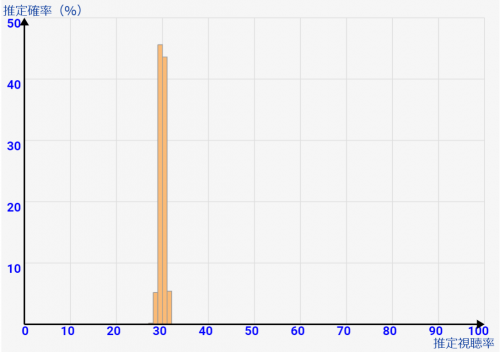
数千レベルのサンプルをとれば、どんなに世帯数が多くても視聴率は1,2%誤差で推定できる!
↑の結果をみるといえるのは「全世帯数が何十億人いようと、5000サンプルぐらいとれば多くても1,2%の誤差に落ち着く」ということです。
サンプル数100とかのレベルでは、結構広がりがある推定視聴率分布になっていますが、サンプル数5000とかになるとほぼ真の視聴率を推定できています。これは、サンプル数がもっと多くてもこうなります。
昔トリビアの泉で、何の調査をするときも「サンプル数2000人ぐらい必要」と仰っていましたが、↑のような収束の原理があるので、そう言っていたんですね!
逆に0.1%の誤差しか許さない場合にはもっと膨大な数を調べる必要がある!
今回は5000人サンプルまでの結果を見てみましたが、逆の見方をすると、分布の収束具合は数が増えるほど緩くなります。↓のようにサンプル数1000と5000を比べると結構収束していますが。。その収束具合は100→1000のときの収束感とくらべると緩くなっています。
[サンプル数=1000]

[サンプル数=5000]

専門的にいうと、誤差範囲を1/2にしたい場合はサンプル数を4倍にする必要があります。つまり、サンプル数5000の誤差を半分にしたい場合は、20000サンプル調査する必要があります。大変ですね><
故に、「ある程度までの誤差レベルなら数千の調査で十分だけど、もっと精度を高めるためには倍々でサンプル数を増やす必要がある」ということなんです!
- 視聴率調査はサンプリング数で正確性がかわってきて、数千レベルの調査で誤差が数%レベルにまで収まる
- 逆にもっと精度が必要な場合は数万レベルの調査を行わないといけない
まとめ動画
⇒「サイコロとクジで学ぶ確率統計」カテゴリ記事一覧
その他関連カテゴリ