「偏ったサイコロの合計値」が正規分布に近づくことをシミュレーターで確認しよう![中心極限定理]
コチラのページにあるサイコロシミュレーター、色々な方に使って頂いて有難いです(o_ _)o
前回は「サイコロの合計値の分布」が、試行回数が増えてくると必ず釣鐘型の「正規分布」に近づくというお話をしました。
今回は、その発展で「偏ったサイコロ」の場合でも成り立つことを確認してみます!
![「偏ったサイコロの合計値」が正規分布に近づくことをシミュレーターで確認しよう![中心極限定理]](https://retu27.com/wp-content/uploads/20220310224831-500x359.png)
目次
おさらい:「サイコロを〇回振った時の合計」はどうなる?
サイコロを〇回振った時の合計が、どのような確率分布になるかを考察していきます。
1回振った時の確率分布
これは簡単で↓のようになります。確率分布とは、「各値になる確率は何%か」をグラフにしたものです。合計すると100%になります。
1回の場合は純粋に、全ての目が同じ確率=1/6=16.666…%になります。ですので、↓のような確率分布になるわけです!

2回振った時の確率分布
2回になると少し状況が変わってきて、↓のようなグラフになります。

なぜならば(1回目,2回目)という書き方をすると↓のように階段状になるからです!
2:(1,1)
3:(1,2),(2,1)
4:(1,3),(2,2),(3,1)
5:(1,4),(2,3),(3,2),(4,1)
6:(1,5),(2,4),(3,3),(4,2),(5,1)
7:(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)
8:(2,6),(3,5),(4,4),(5,3),(6,2)
9:(3,6),(4,5),(5,4),(6,3)
10:(4,6),(5,5),(6,4)
11:(5,6),(6,5)
12:(6,6)
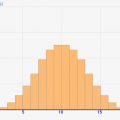
この試行を3回目、4回目と繰り返していくと、、、↓のようになります。
[3回目]

[4回目]

これは「正規分布」と呼ばれる、統計学で一番重要な分布です!
なぜならば、↓のような重大法則があるからです。
どんな確率分布のグラフでも、それを試行する回数を多くするとその平均(合計)は正規分布に近づいていく
今回は「偏ったサイコロ」でこの定理を確認してみます!
「サイコロを〇回振った時の合計」分布をシミュレーターで見てみよう!
それではさっそくシミュレーターを使ってみましょう!
サイコロ出目の指定方法
今回のシミュレーターは、「サイコロの各目の出る比」を指定できます。
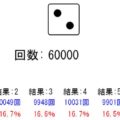
例えば、サイコロの出る目の比を「1:0:3:1:1:4」にすると↓のようになります。指定した比で1~6の目が出るわけです。

↑の通り、0にすると確率0になり、その目が出なくなります。
このように、今回のシミュレーターでは自由にサイコロの目を偏らせることが出来ます!
「偏ったサイコロの合計値」シミュレーター
- ↑の説明の通り、「1~6の目」の出る比率を↓で指定できます。0にすると一切その目は出ないという意味です
- 振る回数を選択すると、「その回数サイコロを振った時の合計値」の確率分布が表示されます
- 回数が多くなっていくと、ほぼ同じ形の分布になっていく事を確認しましょう!
- グラフの縮尺は、観察しやすいように自動で調整されるので、注意して下さい
* サイコロは指定回数振った一例を表示しています。
シミュレーター結果
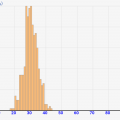
シミュレーターでどのように分布を変えても、50回試行と回数を増やすと、正規分布に近づいていくことが分かると思います!
例として↓のように極端に偏ったサイコロの場合を見てみます。

[4回目] まだすごく偏ってますね
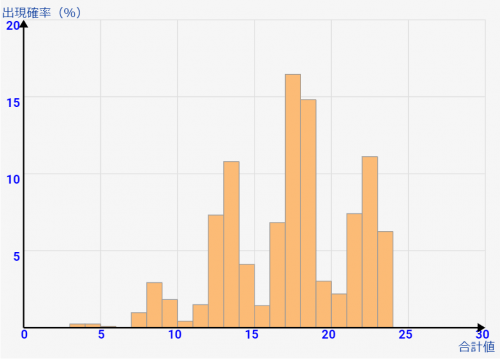
[8回目] 少し近づいてきました

[15回目] 結構、釣鐘型の正規分布に近づいてきて、、、

[30回目] ほぼ正規分布ですが、やや左右で偏りあります

[50回目] 微小量偏りありますが、ほぼ正規分布ですね!

このように、どんなに偏っていても、最終的には正規分布の形に収束していきます。回数を重ねることで、分布が緩やかに混ざり合っていき、最終的に釣鐘型の正規分布になるイメージです!
詳しい証明などは別記事でいつか説明するつもりですが、↓の定理が成り立つことをイメージとして今回のシミュレーターで捉えておきましょう!
どんな確率分布のグラフでも、それを試行する回数を多くするとその平均(合計)は正規分布に近づいていく
- どんなに偏った出目でもサイコロを振る回数を増やしていくと、釣鐘状の「正規分布」に近づく
- これは中心極限定理という重大な統計の法則によるもの
まとめ動画
⇒「サイコロとクジで学ぶ確率統計」カテゴリ記事一覧
その他関連カテゴリ