確率入門]

2022-03-13　

本サイトでは、数学分野の内容を基礎から分かりやすくシミュレーターを用いて解説しています！このベースを用いて、以後「統計学/確率」の分野の内容を同様にシミュレーターを作って解説していきたいと思います！
　
前回までの記事では統計上一番重要な、「平均値」「中央値」の説明をしてきました。これは統計データの「真ん中」を表す概念でした。

それに対して、もう一つ統計学上大事な概念があります。それが「データのバラつき」です。そして、それを表すのが「分散」「標準偏差」という代表値です。本記事では、データのバラつきの意味と「分散」「標準偏差」の定義とイメージを詳しく解説していきます！
データのバラつき(分散/標準偏差)とは何か？をシミュレーターを用いて詳しく解説！実験で深く理解しよう！[統計学/確率入門]

1 データの「バラつき」とは、、、まずは体感してみよう！
- 1.1 シミュレーターで「データのバラつき」を体感して、イメージを掴もう！
- 1.2 データのバラつきのイメージ
2 データのバラつきを表す代表値「分散」「標準偏差」
3 自分でシミュレーターに点数を入力していき、標準偏差の変動のイメージを掴もう！
- 3.1 シミュレーターの概要
- 3.2 標準偏差計算シミュレーターを実際に動かしてみよう！
4 次回は「偏差値」について解説します！

データの「バラつき」とは、、、まずは体感してみよう！

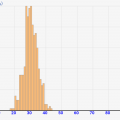
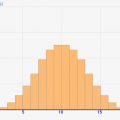
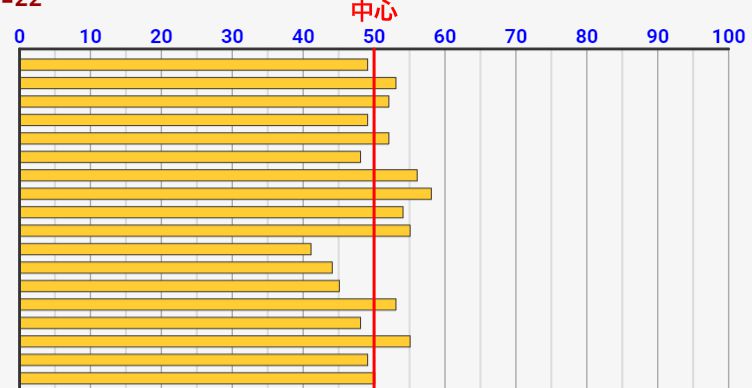
「バラつき」とは何か。それは、どれだけ各データの数値が乱雑になっていてバラついているか、ということです。テスト結果でいうと、みんなが50点であればバラついてないし、皆が40点～60点付近であればある程度バラついていると言えるし、さらに0点の人も多くいて100点の人も多くいる状態であればかなりバラついている、、と言えます。曖昧ですが、そんなイメージです。

シミュレーターで「データのバラつき」を体感して、イメージを掴もう！

上のような曖昧な説明だと分かりにくいので、シミュレーターを使って「データのバラつき」を体感してみましょう！

シミュレーションの説明

スライドバーを動かすとシミュレーターが動きます
スライドバーの乱雑度の数値によって、「バラつき」具合を変えられます
データは50を中心にして出力されます

バラつきが0から最大限まで変えてみて、「バラつき」を体感してみましょう！

乱雑度

データのバラつきのイメージ

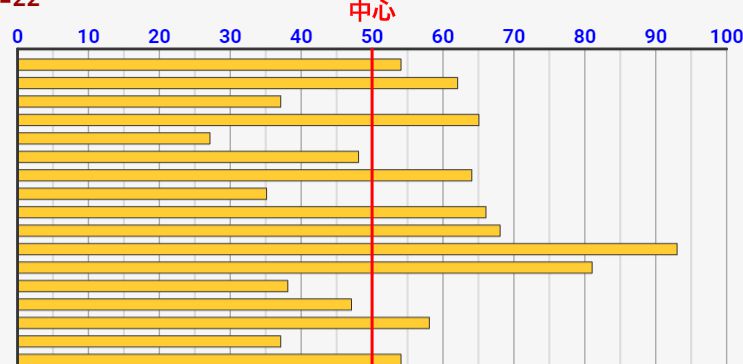
上記のシミュレーターで大体理解できたかと思いますが、各乱雑度での結果のおさらいをしていきます。

[乱雑度=0]

[乱雑度=5]

[乱雑度=20]

この結果を見ると、乱雑度が高くなるほど中心から離れた数値が多くなる傾向にあることが分かります。つまり、「中心からどれだけ離れているか」を数値化できれば、「データのバラつき」が表わせそうですね！
　

POINTデータのバラつき　＝　中心からどれだけ各点が離れているか

データのバラつきを表す代表値「分散」「標準偏差」

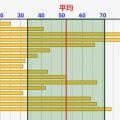
上記の考察の通り、「中心からどれだけ離れているか」を表現できればデータのバラつき度合いを数値で示せそうですね。そこで下図のように「全データに対して、平均値からどれぐらい離れているか」を求めることを考えます。赤い線が平均値で、紫の線がその平均値との差です。この紫の線の長さでバラつきが表わせそうですね！この線の長さの平均値をとると、バラツキ具合が示せそうですね！

　
それでは、バラつきを数式化してみましょう！前回までと同様に以下のように記号を定義します。

n: テストを受けた人数(データ個数)
\(x_i\): i番目の人の点数

そして、平均値(\(\bar x \)とします）は前回記事で解説した通り、以下の式で表せます。

平均値の定義

\( 平均値 \bar x \)
\( \displaystyle = \frac{1}{n}(x_1 + x_2 + … + x_n) \)
\( \displaystyle = \frac{1}{n}\sum_{i=1}^{n}x_i \)

そうすると、上記でいっていた「平均値と各データ値との差異」の平均は以下の式で表せます。

\( データのバラつき度合い \)
\( \displaystyle = \frac{1}{n}\sum_{i=1}^{n}| \bar x – x_i| \)

このようになるんですが、、、数値計算上、絶対値の計算って面倒だったりするんですよね(マイナスとプラスで分岐して計算しないといけない)。そのため、\(| \bar x – x_i|\)を\((\bar x – x_i)^2\)に入れ替える事を考えます。これならマイナスプラスの記号が消えるので。そして、これこそが統計で非常に重要な指標である「分散」の定義になります。この分散は\(σ^2\)という記号で表すことが多いです。

分散の定義

\( 分散σ^2 \)
\( \displaystyle = \frac{1}{n}\sum_{i=1}^{n} (\bar x – x_i)^2 \)

この「分散」こそ、「データのバラつきを表す指標値」なのです！

しかし、一つ問題があります。記号を消すために分散は二乗しています。ですので、下図の紫矢印の長さの二乗の平均値になっているんですよね＞＜

ということで、これを元の次元に戻すためにルートをとります。これが「標準偏差」です。標準偏差は分散のルートなので、\(σ\)という記号で表すことが多いです。

標準偏差の定義

\( 標準偏差σ \)
\( \displaystyle = \sqrt{\frac{1}{n}\sum_{i=1}^{n} (\bar x – x_i)^2} \)

　
この標準偏差を使うと、データがどれぐらいバラついているかが体感的に分かるのです！

大事なのは「分散」も「標準偏差」も、データのバラツキを表す代表値であるということです！ただ「分散 = 標準偏差の二乗」であり、次元が違うことに気をつけて下さい！

分散と標準偏差については後にその性質などを詳しく解説しますが、まずはこの意味合いを捉えることが重要です！
　

POINT分散 = バラつきを2乗して計算したもの
標準偏差 = 分散のルートをとって元の「バラツキ」の次元に戻したもの

自分でシミュレーターに点数を入力していき、標準偏差の変動のイメージを掴もう！

シミュレーターの概要

ここまで解説した内容で分散と標準偏差の定義は理解できたと思います。しかし、実際にどんな数値になるのかイメージがつきにくいですよね＞＜

そこで、数値を入力すると、リアルタイムに標準偏差の範囲を図示するシミュレーターを作りました！

今回もテストの結果を仮定して、0~100点までで値を入力できるようになっています。
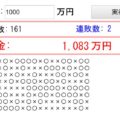
入力したテスト点数により、平均値(赤線)と標準偏差の範囲(緑枠)をリアルタイムに算出して表示します。

緑色の範囲が「標準偏差の範囲内」であり、平均的なデータよりも平均値に近いことを意味しています。逆に緑色の枠外は標準偏差外であり、平均的なデータよりも離れた位置にあることを意味しています！

↓シミュレーターのスクリーンショット。こんな感じで平均値と標準偏差をリアルタイムに図示します！

　

標準偏差計算シミュレーターを実際に動かしてみよう！

それでは、シミュレーターを動かしてみましょう！

[シミュレーションの操作方法]

スライドバーを動かすと、指/マウスを離した時点でその点数が追加されます
データをどんどん入力・追加していき、平均値と標準偏差の変動を確かめて見ましょう
リセットボタンで初期化できます
右上のsdという値が実際の標準偏差の値です

スライドバーを使ってどんどん値を入力し、標準偏差の変化を確かめましょう！

点数

　
「バラつき」と「標準偏差・分散」は↓の関係性にあります。

データをバラついて配置 ⇒ 標準偏差・分散は大きくなる
データを同じようなところに置く ⇒ 標準偏差・分散は小さくなる

次回は「偏差値」について解説します！

本記事では「データのバラつき」について解説しました。「データの中心である平均値からどれだけ離れているか」が「データのバラつき」です。「分散」と「標準偏差」は、「各データと平均値との差異」の平均を計算していくと求められます。この2つを見れば、どれぐらいデータがバラついているかが分かるんですね！
　
次回はこの2つを実践的に応用した概念である「偏差値」について解説します！偏差値はテストなどでよく聞く言葉ですよね。この偏差値、今回解説した「標準偏差」と強い関連があるんです！
　

まとめ