最頻値とは何か？をシミュレーターを用いて詳しく解説！実験で深く理解しよう！[統計学/確率入門]

2020-07-08　 平均/分散等の代表値

本サイトでは、数学分野の内容を基礎から分かりやすくシミュレーターを用いて解説しています！このベースを用いて、以後「統計学/確率」の分野の内容を同様にシミュレーターを用いて解説していきます！
　
前回の記事までで代表値として「平均値」「中央値」について解説しました。これは統計データの「真ん中」を表す概念でした。

統計には「真ん中」を表す概念にもう一つ、「最頻値」というものがあります。これも非常に重要な代表値であり、実は一番汎用性の高い代表値なんです！本記事では「最頻値」をシミュレーターを用いて解説していきます！

「最瀕値」とは一番多く発生した値(項目)のこと！とてもシンプルですが、大事な概念！

前回記事まで数式を用いて、「平均値」「中央値」の説明をしてきました。ですが、「最瀕値」は数式を使う必要もありません。メチャクチャ分かりやすいです！

これだけです。例えばサイコロで例えると分かりやすいです。サイコロを5回振って、2の目が3回、4の目が2回出たとしたら、2の目が最頻値となります！とにかく、最も多く発生したもの＝最頻値なのです！

最頻値は複数あることも…！

この最頻値ですが、複数の値（項目）が該当することもあります。それは、最も多い数（項目）が複数あった場合です。例えばサイコロを4回振って、2の目が2回、4の目が2回出たら、2の目と4の目両方が最頻値になるのです！

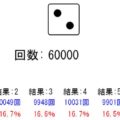
サイコロシミュレーターで「最頻値」を確かめてみよう！

それでは上記の最頻値のイメージを掴むためにサイコロシミュレーターで実験してみましょう！

試行回数を変えて何回か実験してみて下さい！試行回数が小さいと複数の最頻値になりやすいので、その場合も確かめてみましょう！

重要なこと：「最頻値」は数値項目でなくても定義できる！これは平均値や中央値にない特色です！

さて、この非常に簡単な「最頻値」ですが、実はサイコロの目とかテストの点数等の数値的な項目以外でも使えるのです！
　
例えば「好きな食べ物」であったり「出身地」であったり。こういった項目は「ラーメン」「うどん」など、数値じゃない値をとります。数値じゃないので平均値などはもちろん計算できません。しかし、「最瀕値」は決めることは出来ます。みんなが選んだ「好きな食べ物」を調べていって、もっとも回答の多かった項目（食べ物）が最頻値になるのですから！
　
どんなアンケート/統計でも、最頻値は使えるのが最大の特徴です！

　

度数分布表でも使えます！テストの点数など細かい値は階級にまとめよう！

この最頻値ですが、前回説明した度数分布表でも使えます！テスト点数などは、度数分布表に変換してから、最頻値を求めるのが一般的です。

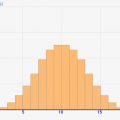
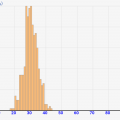
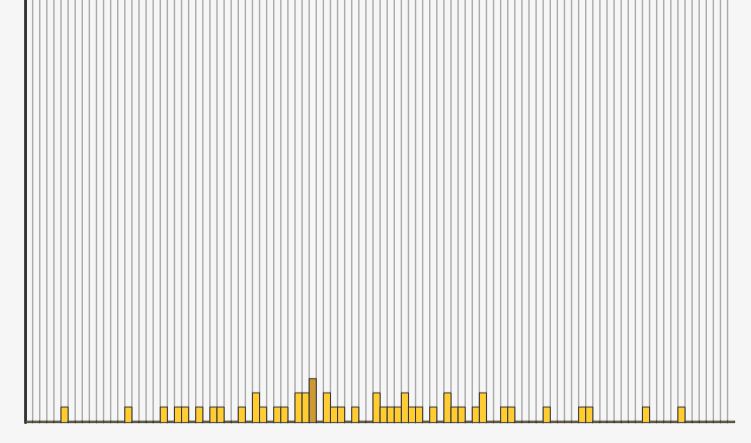
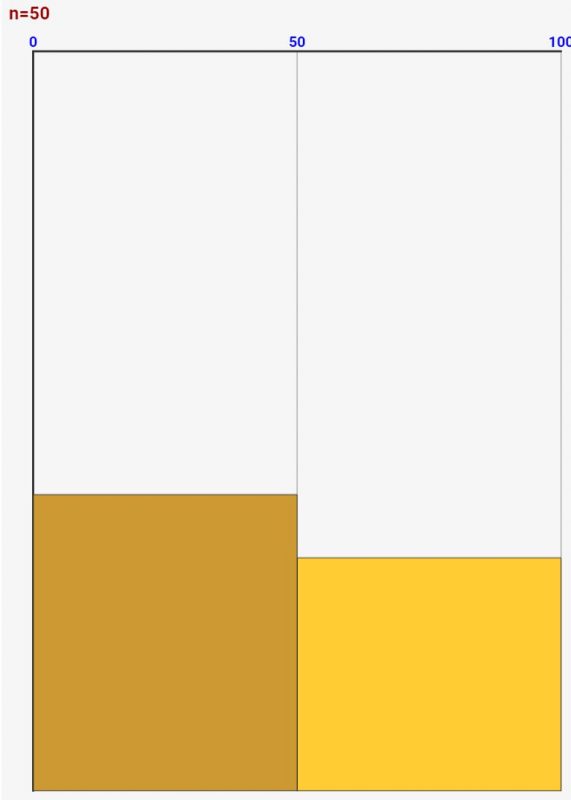
何故ならば、↓のグラフのようにそのままのテスト点数で分布をとってしまうと、細かすぎて、結局どの辺りの点数が多いのかよく分からなくなってしまうからです＞＜　

これに対して、↓のように適当な大きさで度数をとれば、傾向がつかみやすくなり、最頻値が分かりやすくなります。

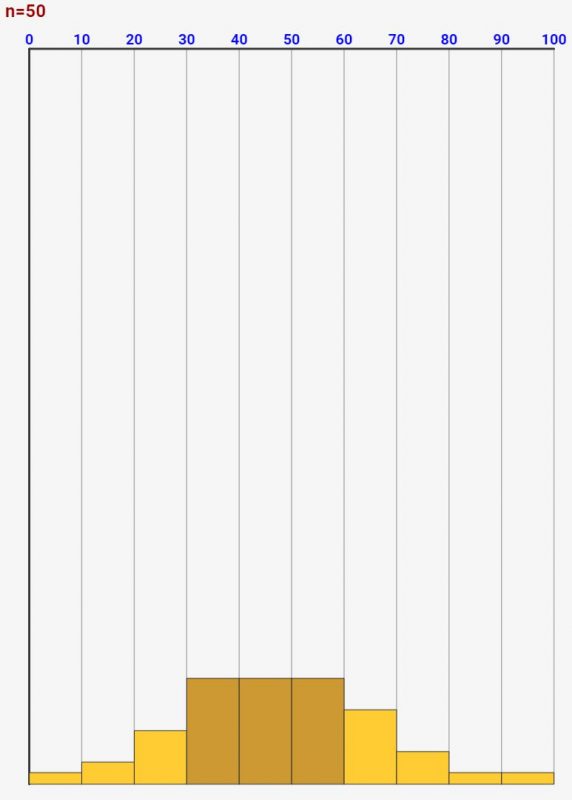
逆に、階級区分をまとめすぎてもよく分からなくなってきます。↓は2段階での区分ですが、これだと全く点数の傾向が分からないですよね！なので、適当な区分で階級をとって度数分布表を作ることが大事なのです！

シミュレーターで階級幅を変えて、最頻値の変化を確かめよう！

上記のような度数分布表/階級区分による最頻値の変化を確かめるためにシミュレーターを用意しました！

色々区分を変えてみましょう！点数は変わらなくても、階級幅によって全くグラフや最頻値が変わってくることを確かめましょう！

次回は「尺度水準」について解説します！

これまで、統計の真ん中を表す代表値として「平均値」「中央値」「最頻値」について解説してきました。同じ「真ん中」を表す概念ですが、定義は全く異なります。そして、今回言及したとおり、実は使える場合もそれぞれ違います。
　
では、どういった場合に各代表値が使えるのでしょうか。その解説のため、次回は統計の「尺度水準」について解説します！どのような統計かを尺度で分けることで、使える代表値を決定出来るんです！乞うご期待！
　

[関連記事] 統計学/確率入門：平均/分散等の代表値

1．平均値

2．中央値

3．分散、標準偏差

4．偏差値

5．度数分布表/階級

6．最頻値(本記事)

7．尺度水準