倍プッシュ(マーチンゲール法)シミュレーションツール!必勝法 倍プッシュの欠点とは!?
倍プッシュ(マーチンゲール法)とは?
倍プッシュとはアカギという漫画(カイジと同じ福本伸行さんの作品)で出てくる必勝法です。簡単にいうと「勝負に負けるごとに、その倍の額を賭けて負け額を必ず取り戻すようにする」賭け方です。
例えば1万円最初に賭けて負けた場合、次は2万円を賭けるわけです。そうすると、勝てれば2万円が返ってきて、負けを取り戻せるです。そこでもさらに負けた場合は、4万円、8万円、16万円と倍の額を賭けていきます。そうするとあら不思議。どこかで勝てれば、必ず負けが取り戻せ、さらに1万円の利益が出ます。
例えば16万円賭けた時には、既に(1+2+4+8)=15万円失っていますが、次に16万円の賭けで勝てれば1万円の利益になるわけです。
このような賭け方、最小単位(ここでは1万円とします)でかける手法を一般的にマーチンゲール法と呼ぶそうです。これ、永遠に繰り返していたら・・・負けないですよね?これならば、必ず毎回1万円勝てて永遠やっていれば億万長者!?と思ってしまいますよね!

倍プッシュ(マーチンゲール法)の落とし穴
しかし、賭け事にそんな簡単な必勝法なんてないはずなんです。では、倍プッシュ(マーチンゲール法)の欠点は何かというと…1)資金が有限であること、もしくは2)賭け場が賭け上限値を設定していることです。
資金が有限だと何故負けるのか。それは単純です。例えば100万円が軍資金の場合、6回連続で負けると64万円を賭けなければいけません。しかし、それまでに63万円投資しているわけで、そのお金は払えないわけです。つまり、100万円しかない場合、6連続負けた時点でアウトです。じゃあ、1000万円ならどうかというと、指数関数的にお金がいるので、9回目の512万円賭けができなくなります。これは2^3=8からもわかる通り、10倍払っても3,4回しか耐えられる限度が延びないんです。まあ、9回連続で負ける確率は0.2%程度の確率なので低いと言えば低いですが…
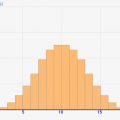
これをわかりやすくいうと、↓のような状況となっています。まず普通にかけた場合は、1/2で1万負け、1/2で1万勝ちです。
[通常の賭けの利益と確率]
1/2:+1万
1/2:-1万
これを、1000万で9回連続負け=(1/512)まで耐えられるように倍プッシュ(マーチンゲール法)で掛けた場合は下記のようになります。
[倍プッシュ時の利益と確率]
511/512:+1万
1/512:-511万
ここで、倍プッシュ(マーチンゲール法)時の期待値を計算すると、「(1*511/512) – (511*1/512) = 0」です。つまり期待値は変わらず0。これは「倍プッシュ(マーチンゲール法)は、通常1/2で負けるものを、1/512まで負ける確率を下げさせる手法。ただしその分、負けた時の損失は大きく、期待値は変えられない」ということです。
つまり、実はこの倍プッシュ(マーチンゲール法)は必負法でもあるんです!長期的な目線から見てですが。
倍プッシュ(マーチンゲール法)をシミュレーターで体験!
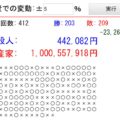
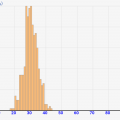
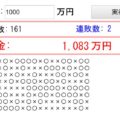
上記の考察を実体験するために、シミュレーターを作ってみました!これは1単位掛け金を1万円として、倍プッシュの賭け方でどこまで資金を伸ばせるか体験するものです!
軍資金を設定できるので、どの程度の金額を持っていれば、どれぐらい耐えられるのかがなんとなく体感的に分かるかと思います!
↓軍資金を入れて、実行ボタンを押してください!シミュレーターが稼働します!
⇒「統計学/確率」カテゴリ記事一覧
その他関連カテゴリ




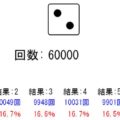


[…] retu27さんという方が運営しているサイトですが、色々なシミュレーターを自作して分かりやすい説明もついてます。マーチンゲールシミュレーター2はコチラ […]