数学入門:「和集合」「積集合」の概念をシミュレーターを用いて解説!
本カテゴリでは数学の「集合」と「命題」について解説していきます。集合とは「何らかの条件にあてはまる要素の集合」です。そして「命題」とも深く関わりがあります。日常生活とも密接に関係のあるお話になりますので、集合の基礎イメージを理解しておきましょう!
本サイトではシミュレーターを用いて「集合」「命題」のイメージをシミュレーターを用いて分かりやすく解説していきます!シミュレーターで実験して、その概念を深く理解して頂ければと思います!
今回は、前回までの集合の基礎の話を前提として、「和集合」「積集合」の概念についてシミュレーターを用いて解説していきます!
目次
集合の基礎のおさらい
まずは集合の基礎について再度おさらいです。集合とは以下のような「何らかの条件に当てはまる要素を集めたもの」です。
「1以上10未満の整数」の集合:1,2,3,4,5,6,7,8,9
「空を飛べない鳥」の集合:ペンギン,ダチョウ,エミュー,ドードー,…
こういったように、「なんらかの条件がついた1つの集合と、それにあてはまる複数の要素」という関係になっており、数学記号で以下のように表します。
全体集合U内の要素xを集合Aが含む場合、
\( \large x \in A \)
と表す。
「和集合」とは、2つの集合を合体させた集合のこと!
それでは今回の本題の一つ「和集合」について解説していきます。和集合とは簡単にいうと「集合Aと集合Bを合体させた集合」のことです。
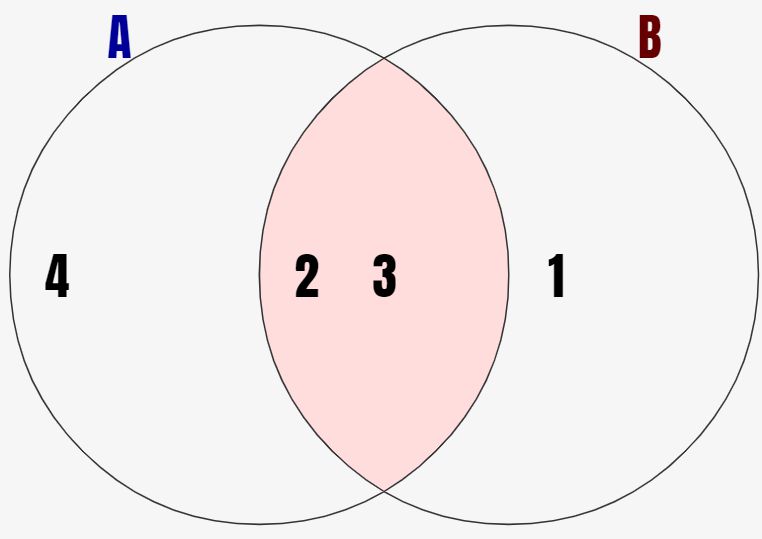
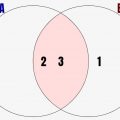
↓の例では集合A={2,3,4} 集合B={1,2,3}となっています。このときにこの2つを合わせた赤背景の領域が和集合になります。
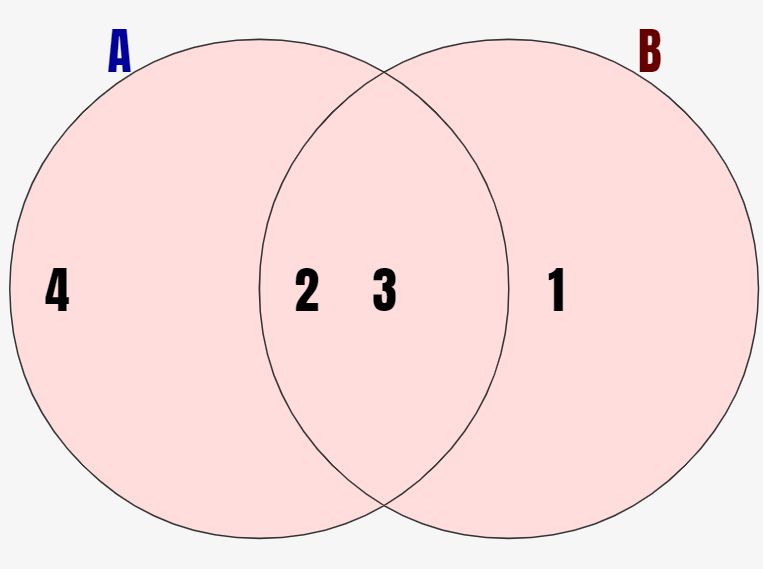
合わせたというのは「Aの要素とBの要素をかき集める」という意味です。AもしくはBに入っている要素は、和集合に含まれるということです。数学的に定義すると、以下の通りです。
全体集合U内の各xに対して、
\( x \in 集合A \)
もしくは
\( x \in 集合B \)
となる時、xはAとBの和集合に含まれる。
そして、その和集合を\(A \cup B \)で表す
つまり、逆にいうと、和集合に含まれる要素xは、集合Aもしくは集合Bどちらかには絶対に含まれているはずなのです。ですので↓の関係が成り立ちます。
「和集合=集合Aと集合Bの合成」というイメージを掴んでおけば大丈夫です!
シミュレーターで「和集合」の関係を理解しよう!
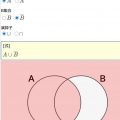
ここでさっそく和集合の概念のイメージをつけるためにシミュレーターで確認してみましょう!
- 集合Aに入る要素と集合Bに入る要素を、チェックボックスで選択することが出来ます
- チェックボックスのON/OFFを切り替えると、↓の図に集合Aと集合Bの関係が反映されて表示されます
- 赤背景で示された範囲が、AとBの和集合です
- 全体集合U={1~9の自然数}の条件で表示します
色々、要素を切り替えて、集合Aと集合Bがどういう和集合を作り上げるか確かめてみましょう!
集合A要素の選択
1 2 3 4 5 6 7 8 9
集合B要素の選択
1 2 3 4 5 6 7 8 9
「積集合」とは、2つの集合の共通部分を表す集合のこと!
それでは次に「積集合」について解説していきます。積集合とは簡単にいうと「集合Aと集合Bの共通部分を表す集合」のことです。絵にすると、分かりやすいので例を。
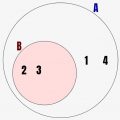
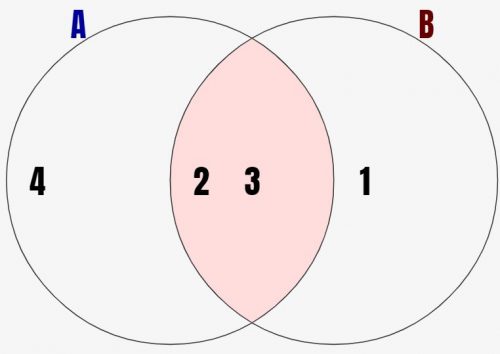
↓の例では集合A={2,3,4} 集合B={1,2,3}となっています。このときにこの2つを合わせた赤背景の領域が積集合になります。和集合と違って、共通部分だけの赤色がついてます。
共通要素とは、集合Aと集合Bともに含んでいる要素xになります。数学的に積集合を定義すると、以下の通りです。
全体集合U内の各xに対して、
\( x \in 集合A \)
かつ
\( x \in 集合B \)
となる時、xはAとBの積集合に含まれる。
そして、その積集合を\(A \cap B \)で表す
つまり、逆にいうと、積集合に含まれる要素xは、集合Aと集合B両方に絶対に含まれているはずなのです。ですので↓の関係が成り立ちます。
和集合と違って、積集合は両方の集合に要素が含まれていないといけないため、和集合より狭い集合になります。「積集合=集合Aと集合Bの共通部分」というイメージを掴んでおけば大丈夫です!
シミュレーターで「積集合」の関係を理解しよう!
ここで和集合と同じく、積集合の概念のイメージをつけるためにシミュレーターで確認してみましょう!操作方法は↑の和集合シミュレーターと同じです。
- チェックボックスのON/OFFを切り替えると、↓の図に集合Aと集合Bの関係が反映されて表示されます
- 赤背景で示された範囲が、AとBの積集合です
- 全体集合U={1~9の自然数}の条件で表示します
色々、要素を切り替えて、集合Aと集合Bがどういう積集合を作り上げるか確かめてみましょう!
集合A要素の選択
1 2 3 4 5 6 7 8 9
集合B要素の選択
1 2 3 4 5 6 7 8 9
和集合/積集合は3つ以上になった時にも、同様の考えを適応すればOK!
上記で説明した和集合/積集合ですが、3つ以上の集合で考えるときも考え方は同じです。
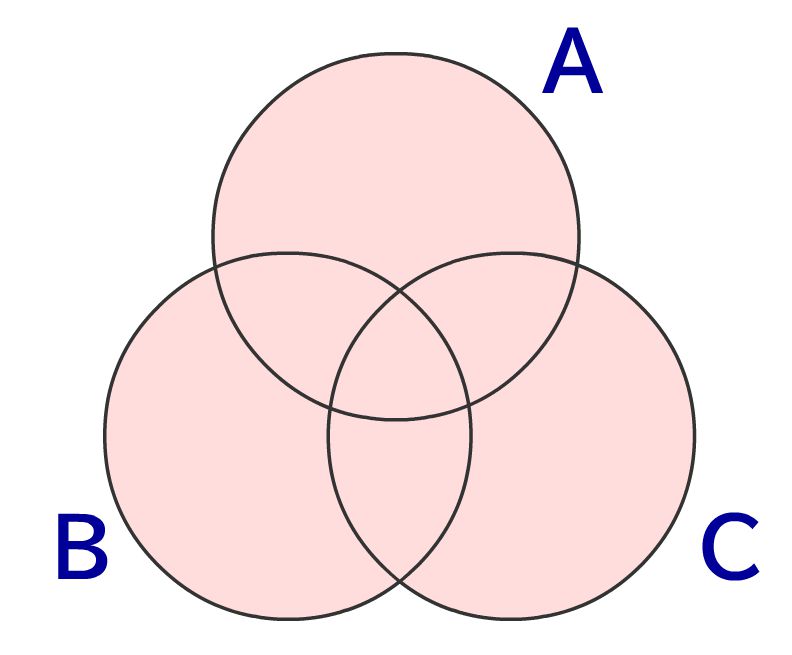
和集合\( A \cup B \cup C \)は3つの集合を合体させた部分を表す集合に!
3つの集合の和集合を考える時は、2つの場合と考え方は同じです。3つの和集合\( A \cup B \cup C \)は集合A集合B集合Cの全ての領域を合わせた領域になります!
→ \(x \in A\) または \(x \in B\) または \(x \in C\)
→ \( A \cap B \cap C \)は全ての集合の合成部分
もちろん、これは4つ5つとなっても同様です。和集合は、全ての集合を合体させた集合になります。
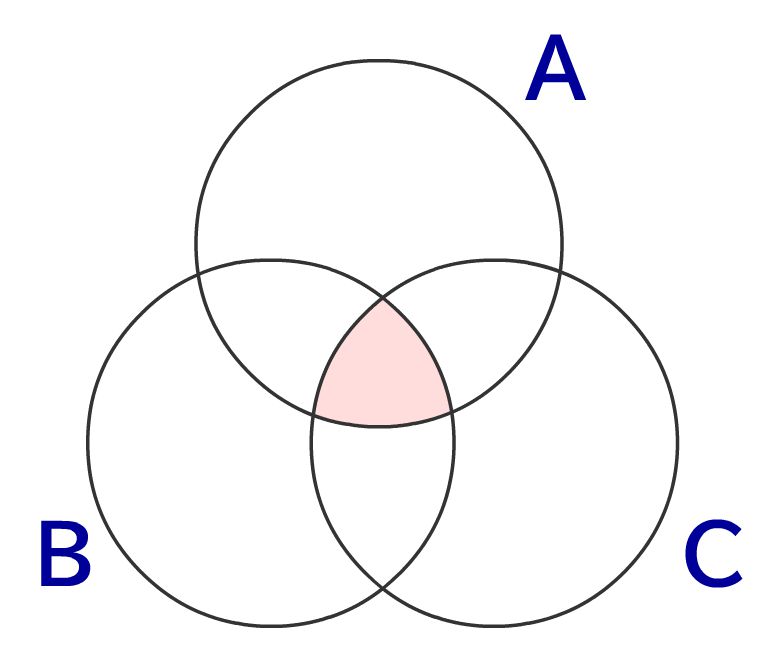
積集合\( A \cap B \cap C \)は3つの集合の共通部分を表す集合に!
積集合も同じです。2つの場合と考え方は同じです。3つの和集合\( A \cap B \cap C \)は集合A集合B集合Cの全ての領域の共通領域を表すことになります!
→ \(x \in A\) かつ \(x \in B\) かつ \(x \in C\)
→ \( A \cap B \cap C \)は全ての集合の共通部分
次回はド・モルガンの法則について解説していきます!
今回は前回の発展として部分集合/積集合について解説しました!
和集合は、「集合Aと集合Bを合体させた集合」です。集合Aと集合B、どちらかに含まれる要素は和集合でも含まれます。
それに対して、積集合は、「集合Aと集合Bの共通領域を抽出した集合」です。集合Aと集合B、療法に含まれる要素だけが積集合の要素になります。
次回はこの和集合積集合の演算をするときに便利な、「ド・モルガンの法則」についてシミュレーターを用いて解説していきます!
- A,Bの和集合 = A,B含めた全体領域
- A,Bの積集合 = A,Bの共通領域
⇒「集合と命題」カテゴリ記事一覧
その他関連カテゴリ