「部分集合」の概念をシミュレーターを用いて解説！[数学入門]

2021-02-27　 集合と命題

本サイトではシミュレーターを用いて「集合」「命題」のイメージをシミュレーターを用いて分かりやすく解説していきます！シミュレーターで実験して、その概念を深く理解して頂ければと思います！

今回は、前回の集合の基礎の話と補集合の発展として、部分集合の概念についてシミュレーターを用いて解説していきます！

集合の基礎のおさらい

まずは集合の基礎について再度おさらいです。集合とは以下のような「何らかの条件に当てはまる要素を集めたもの」です。

こういったように、「なんらかの条件がついた1つの集合と、それにあてはまる複数の要素」という関係になっており、数学記号で以下のように表します。

「部分集合」とは、包含される集合のこと！

それでは今回の本題の「部分集合」について解説していきます。部分集合とは「集合Aに包含される小さな集合B」のことです。

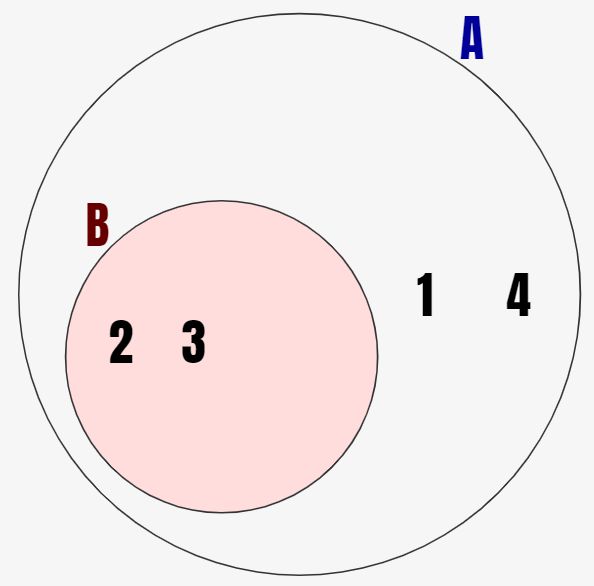
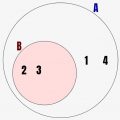
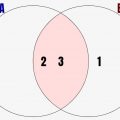
例でいうと↓のような感じです。この図は大きい円が集合A、小さい円が集合Bを表しています。つまり、改めて要素列挙すると

となっています。

つまり、集合Aのほうが要素が多く、さらに集合Bの要素2,3は全て集合Aに含まれています。こういった時に、集合Aは集合Bを包含しているため、集合Bは集合Aの部分集合と言えます。

「部分集合」の数学的定義

この部分集合、数学的な定義を書くと以下の通りになります。

Bが持つ要素を、Aが全て含んでいたら部分集合ということですね！その時、\( B \subset A \)と記号で表します。不等号の変形バージョンで、口が開いたほうが大きい集合とイメージすると、覚えやすいと思います。
　

「部分集合」の注意点2つ！

↑の解説で部分集合とは何かを説明しましたが、2点だけ少し注意が必要なパターンがあるので説明しておきます。

注意点1:集合B=集合Aでも、BはAの部分集合

これは直感に反することですが、もしも集合Bと集合Aが同じでも、BはAの部分集合となります。（同じとは、集合Aに含まれる要素と集合Bに含まれる要素が全て同じということです）

集合Aと集合Bが同じ時の例

これは、上記の定義に立ち返ればわかります。

これは集合Bと集合Aが同一の場合でも成り立ちまよね。Bの要素xを集合Aは余すことなく含んでいるので。ですので\( B \subset A \)となります。

で、逆にいうと\( A \subset B \)でもありますよね。同じ立場なんですから、AもBの部分集合なんです。

これをまとめると、以下のようなことが言えます。

直感的にいうと、、、AがBを包含していて、BがAが包含しているなら、それはもうAとBは同じってことです！

注意点2:空集合も部分集合に入る

これもかなり直感と食い違うことです。もし集合Bが空集合であっても、集合Aの部分集合と言えます。

集合Bが空集合の場合

これも定義に立ち返ってみましょう。

今、\( B = 空集合\emptyset \)であり、\( x \in B \)を満たすxはありません。そのため、どんな集合Aでも、この条件を満たすのです！
つまり、

と言えます。さらに空集合自体も集合の一種なので、

と言えます。空が空を持つってどういうこと？？って思いますが、数学的な定義としては正しいと言えるのです(*^_^*)
　

シミュレーターで「部分集合」の関係を理解しよう！

ここで部分集合の概念のイメージをつけるためにシミュレーターで確認してみましょう！

色々、要素を切り替えて、集合Aと集合Bがどういったときに部分集合になるのか確かめてみましょう！
集合A要素の選択
1 2 3 4 5 6 7 8 9
集合B要素の選択
1 2 3 4 5 6 7 8 9

次回予告：和集合・積集合について解説していきます

今回は、前回の発展として、部分集合について解説しました！部分集合は、「集合Aに包含される集合B」という関係を示す言葉です。基本的には部分集合Bは集合Aよりも小さいはずですが、その定義から集合Bが空集合となることもあるし、集合B＝集合Aのときもあることに注意して下さい。
　
次回は、2つの集合の関係を考える時に重要な、「和集合/積集合」についてシミュレーターを用いて解説していきます！
　

[関連記事] 数学入門：集合と命題

1．集合/全体集合/空集合

2．補集合

3．部分集合(本記事)

4．和集合/積集合

5．ド・モルガンの法則

6．命題/集合との関係/必要条件と十分条件

7．命題の逆/裏/対偶の関係

8．論理和/論理積/全称命題/存在命題の否定