「命題の逆/裏/対偶の関係」を、図式を用いて解説![数学入門]
本記事では数学の「命題の逆/裏/対偶」について解説していきます。前回の記事まで数学の集合に関する説明をシミュレーターを用いてしてきました。本記事からは、その考えを応用して「命題」について解説していきます!
命題は、日常的にも出てくる概念です。そして間違った知識でこの命題を扱うと、論理的に間違った結論が出てしまったりします><ですので、数学関係なくとも命題に関する正しい知識を身に着けておきましょう!
本記事では前回記事で説明した命題について、その命題の逆/裏/対偶について説明していきます!これを意識できるようになると、論理的思考が捗りますよ!
![「命題の逆/裏/対偶の関係」を、図式を用いて解説![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200712195321-1-500x333.jpg)
目次
命題とは?のおさらい
まず命題とは何かの復習です。
「正しい(真)」か「正しくない(偽)」か明確に客観的に決められる文や式
ということでした。これに対して、多くの命題は以下のように\(p \Rightarrow q\)の形式で表せます。
鳥 \(\Rightarrow\) 空を飛べる
愛知県 \(\Rightarrow\) 日本一人口が多い県
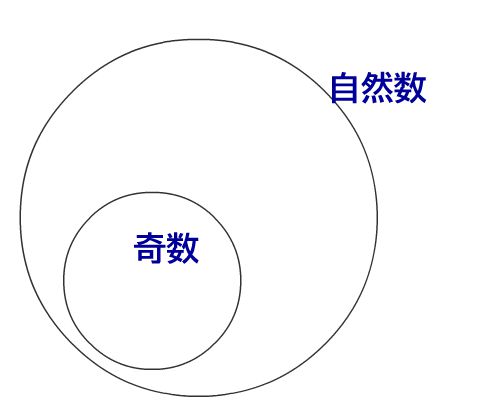
奇数 \(\Rightarrow\) 自然数
\(x^2 < 4\) \(\Rightarrow\) \( -2 < x \)
このような形式で表せるとき、実は命題は集合論的に考えることができます。もしも\(p \subset q\)、つまり条件pが結論qの部分集合なら、この命題は真ということができます!つまり、pとqの大小関係を比較することが、命題の真偽を決めるわけです!
↓このような部分集合の関係があるとき、\(p \subset q\)といえる
命題の逆/裏/対偶を考えよう!
それでは、今回の主題である命題の逆/裏/対偶について解説していきます!
今までと同じく命題「\(p \Rightarrow q\)」について考えます。このとき、逆/裏/対偶は以下のように表せます。
↓
逆:\( \large q \Rightarrow p\)
裏:\( \large \overline{p} \Rightarrow \overline{q}\)
対偶:\( \large \overline{q} \Rightarrow \overline{p}\)
このように、元の命題:\(p \Rightarrow q\)に対して3つの変形があるわけです!
わかりやすくするために、
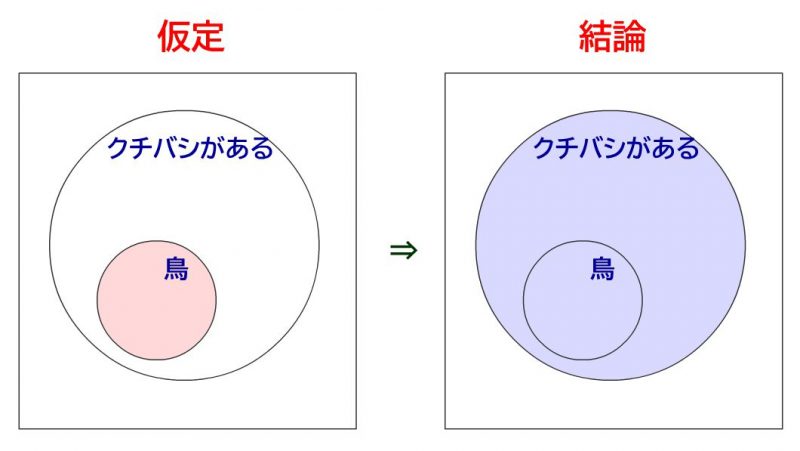
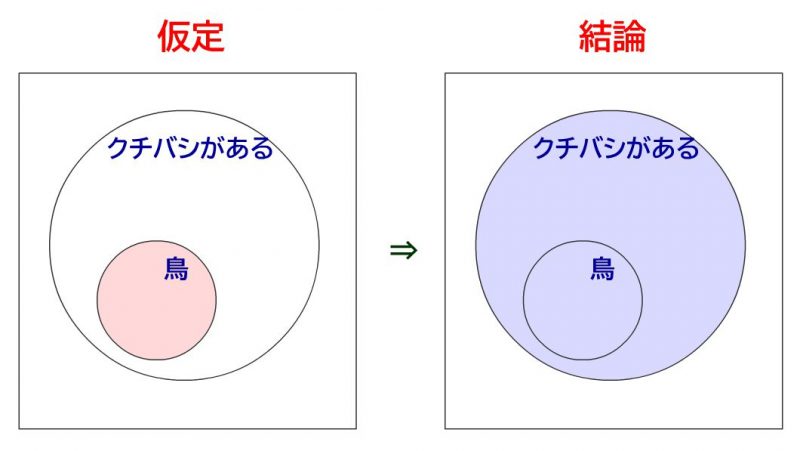
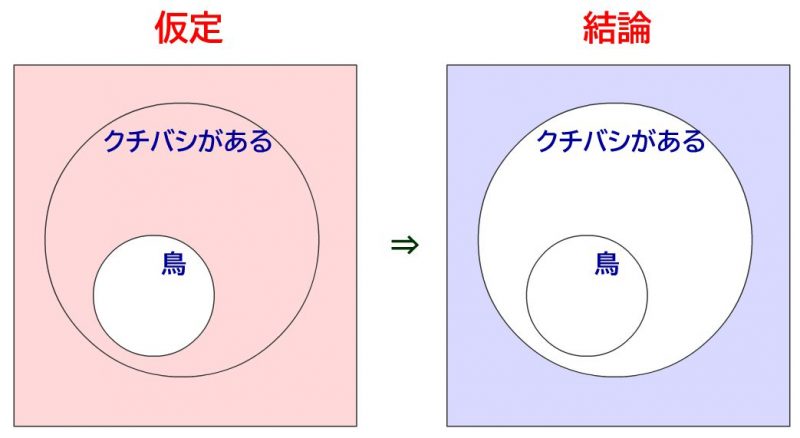
元の命題: 「鳥ならば、クチバシがある」
を考えます。とりあえず、この命題は真です。全ての鳥にはクチバシがあります。なので絵にすると↓のような感じです。以下、仮定を赤色、結論を青色で図で示していきます
で、逆/裏/対偶は以下のようになります。
逆:「クチバシがあるならば、鳥である」
裏:「鳥でなければ、クチバシはない」
対偶:「クチバシがなければ、鳥ではない」
日本語で書くとこんな感じ。どれも似ているようですが、違います。
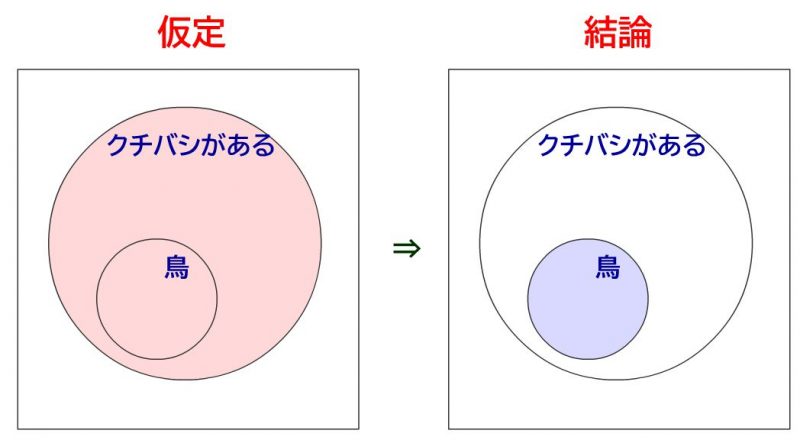
逆:「クチバシがあるならば、鳥である」
これは全く命題とは違うことを言っています。「クチバシがある動物は、全て鳥である」といっているんですね。これは偽です。鳥でなくても、カモノハシなどが哺乳類でも朽クチバシもっているので。
なので絵にすると↓な感じです。仮定条件(赤色)のほうがおおきくて、必ずしも青色の部分に入らない要素(カモノハシ)があるわけですね!
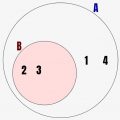
裏:「鳥でなければ、クチバシはない」
これもまた命題とは違いますよね。「鳥以外の動物は、クチバシを持っていない」といっているんです。図にすると↓のようになります。鳥集合以外の領域(赤色)が仮定条件であり、クチバシがある集合外(青色)が結論の集合になっています。これは偽となります。なんか逆と似ていますね。というか、「逆と裏は全く同じことを言っている」んです!詳細はこの後!
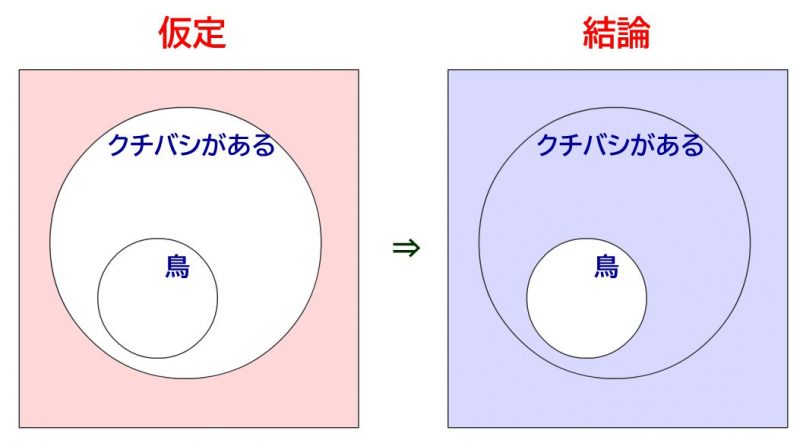
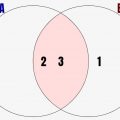
対偶:「クチバシがなければ、鳥ではない」
問題はこの対偶です。クチバシがなければ、鳥ではない、、、なんか命題の「鳥であれば、クチバシがある」と同じこといってそうですね。
そのため、図解すると、↓のようになります。クチバシがある集合外の赤い領域(紫野領域)が前提であり、鳥以外の動物の領域が青色で示されています。仮定条件の赤い領域を、結論の青い条件が包含していますよね。なので、この対偶は真となります。
「命題の対偶が真⇔命題が真」「命題の対偶が偽⇔命題が偽」といえる!
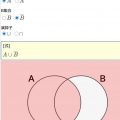
実は、元の命題と対偶命題の真偽は同じになるんです!それは、以下の図からもわかると思います!
元の命題「\(p \Rightarrow q\)」を考えたとき、「\(p \subset q\)」となり、pがqの部分集合となれば真でした。
このときに、上の図のように補集合\( \overline{q} \)は\( \overline{p} \)に必ず包含されます。つまり、「\(\overline{q} \Rightarrow \overline{p}\)」は真となります。
何故ならば、\( x \notin q \Rightarrow x \in p \)である要素xがあると仮定すると、「全てのxに対して\( x \in p \Rightarrow x \in q \) 」という事実と矛盾するからです!(これは背理法的な考え方。後日解説します!)
このため、「命題の真偽を判定するため、代わりに対偶を考えて真偽を判定する」ということも可能なのです!
命題が証明しにくかったら、対偶を考える!これは素晴らしい証明テクニックです!
命題の逆/裏/対偶の関係図
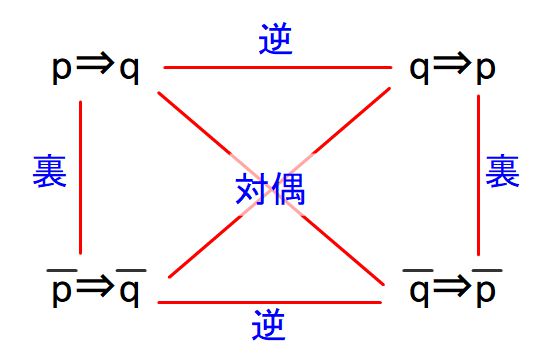
最後に、命題の逆/裏/対偶のとの関係図を示します。実は4つの命題は↓のような関係になっています。
実は「命題の逆 \(q \Rightarrow p\)」と「命題の待遇\(\overline{q} \Rightarrow \overline{p}\)」は裏の関係になっており、「命題の裏\(\overline{p} \Rightarrow \overline{q}\)」と「命題の待遇\(\overline{q} \Rightarrow \overline{p}\)」は逆の関係になっています。
そして重要なのが、「命題の逆\(q \Rightarrow p\)」と「命題の裏\(\overline{p} \Rightarrow \overline{q}\)」は実は対偶だということ!つまり、「命題の裏の真偽⇔命題の逆の真偽」なんです!この2つは同じ値になるんですね!
つまり、命題的には元/逆/裏/対偶の4つあるように見えますが、実は命題の真偽としては2種類しかないんです。その真偽は集合pと集合qの部分集合関係によって決まります。どちらがどちらの部分集合になるかで真偽が決まってくるんですね!
集合p=集合qのとき、元/逆/裏/対偶は全て真となる!
さて、上記のように真偽は2つの種類しかないという結論なんですが、、、特に集合pと集合qが同一だった場合は特別です。このときには\(p \subset q\)も\(q \subset p\)も成り立つので、結局、元/逆/裏/対偶の全てが真になります!
これは、前回の命題の基礎で説明した「pとqがともに必要十分条件になるとき」になります!pとqが同一になるときのみ、これが成立するんですね!

まとめ:命題の対偶をとって楽をしよう!
最後にまとめです。今回は数学の命題の元/逆/裏/対偶について考えてきました。4つの種類について説明しましたが、結局は2種類しか真偽はありません。
↓のような関係になっており、「元の命題」と「対偶」、「裏」と「逆」はそれぞれ対偶関係になっています。そして、対偶関係になっている命題は実は真偽が一緒になるんです。ですので、命題がわかりにくかったら、対偶をとってみるのが良いかもですね!
この対偶をとるためには、仮定p,結論qの否定/補集合を考える必要があります。そのため、次回は各条件の補集合を考えるときにどうすればいいか説明していきます!論理和/論理積や、全称命題/存在命題について説明し、その後その否定について解説していきます!

- 命題\(p \Rightarrow q\)には、それに対応した逆/裏/対偶の命題があるがある。
- 実は対偶は元の命題と同値。対偶を証明すれば、元の命題の証明になる
- 全ての命題が成り立つ時、p = qといえる
⇒「集合と命題」カテゴリ記事一覧
その他関連カテゴリ