集合のド・モルガンの法則をシミュレーターを用いて解説![数学入門]
本カテゴリでは数学の「集合」と「命題」について解説していきます。集合とは「何らかの条件にあてはまる要素の集合」です。そして「命題」とも深く関わりがあります。日常生活とも密接に関係のあるお話になりますので、集合の基礎イメージを理解しておきましょう!
本サイトではシミュレーターを用いて「集合」「命題」のイメージをシミュレーターを用いて分かりやすく解説していきます!シミュレーターで実験して、その概念を深く理解して頂ければと思います!
今回は、前回までの集合の基礎の話や「和集合」「積集合」を発展させた、「ド・モルガンの法則」という定義をシミュレーターを用いて解説していきます!
![集合のド・モルガンの法則をシミュレーターを用いて解説![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200712154358-423x500.jpg)
目次
集合の基礎と補集合/和集合/積集合のおさらい
集合の基礎
まずは集合の基礎と和集合/積集合について再度おさらいです。集合とは以下のような「何らかの条件に当てはまる要素を集めたもの」です。
「1以上10未満の整数」の集合:1,2,3,4,5,6,7,8,9
「空を飛べない鳥」の集合:ペンギン,ダチョウ,エミュー,ドードー,…
こういったように、「なんらかの条件がついた1つの集合と、それにあてはまる複数の要素」という関係になっており、数学記号で以下のように表します。
全体集合U内の要素xを集合Aが含む場合、
\( \large x \in A \)
と表す。
補集合のおさらい
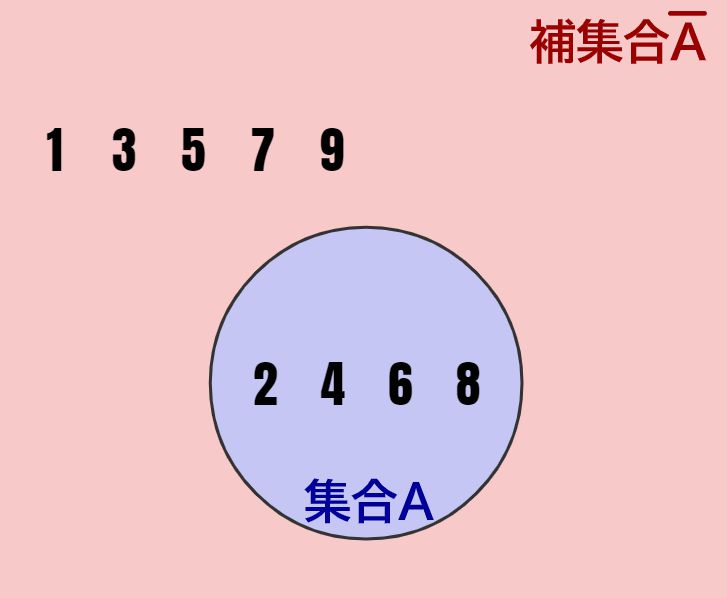
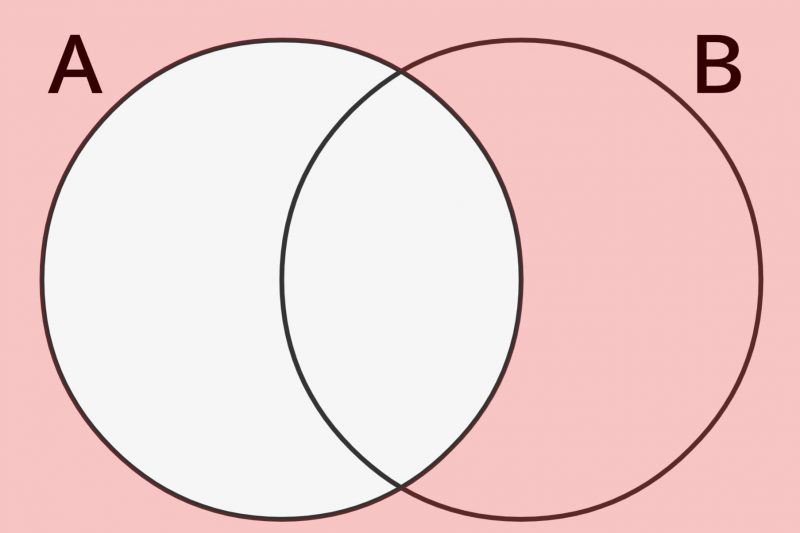
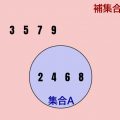
補集合は、集合Aの反対をとった集合です。わかりやすくいうと、集合Aに含まれない要素を集めたのが補集合\(\overline{A}\)です。↓の図の赤い部分が補集合\(\overline{A}\)になります。
式にすると↓を満たします。集合Aが含まない要素を全て含んだ集合が補集合\(\overline{A}\)です。
\( x \in A \Rightarrow x \notin \overline{A} \)
和集合のおさらい
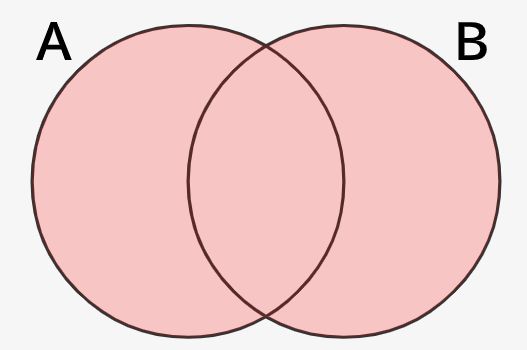
和集合は集合Aと集合Bを合わせた領域を示す集合です。図で見るとわかりやすく、コチラの例では↓赤背景で示した部分が和集合になります。
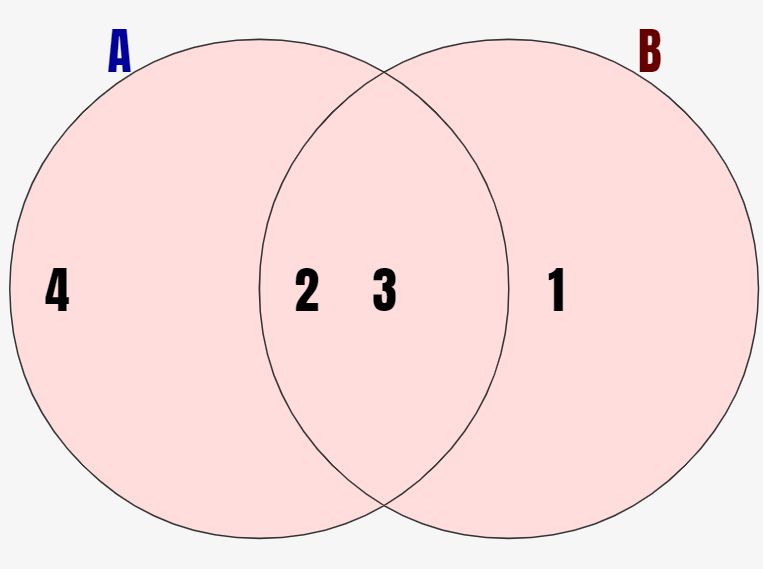
集合Aと集合Bの和集合は\(A \cup B\)という形式で表します。そして和集合の要素は下記のように、集合Aもしくは集合Bが含んでいることが条件になります。どちらかの集合が含んでいればOKなんですね!
積集合のおさらい
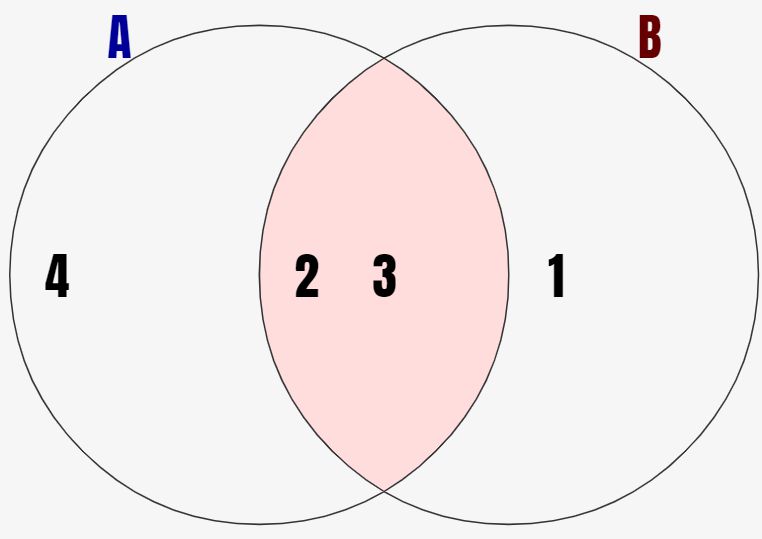
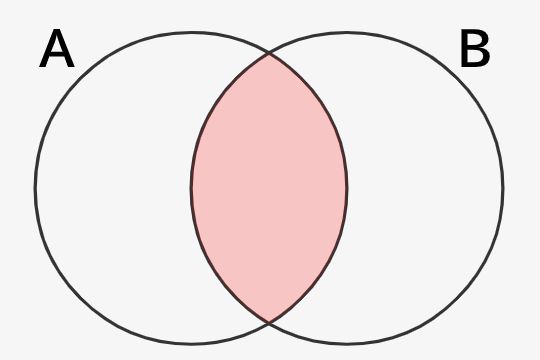
積集合は集合Aと集合Bの共通領域を示す集合です。図で見るとわかりやすく、コチラの例では↓赤背景で示した部分が積集合になります。つまり、AとBの共通領域です。
集合Aと集合Bの積集合は\(A \cap B\)という形式で表します。そして積集合の要素は下記のように、集合Aと集合Bがともに含んでいることが条件になります。両方の集合が含んでいることが必要で、和集合より条件が厳しくなっています。
ド・モルガンの法則とは?
それでは、ここからド・モルガンの法則について解説します。ド・モルガンの法則は以下の定理のことです。
[法則1]
\( \large \overline{ A \cup B} = \overline{A} \cap \overline{B} \)
[法則2]
\( \large \overline{ A \cap B} = \overline{A} \cup \overline{B} \)
以下この法則解説していきます!
ド・モルガンの法則1の解説
ちょっとこの式を見ただけだと分からないので解説していきます。まず法則1から。上線は補集合をとるという意味です。すなわち、和集合\(A \cup B\)の補集合は、実は補集合\(\overline{A}\)と補集合\(\overline{B}\)の積集合と同一である事を表してるんです!わかりにくいので絵でみてみましょう。
これに対して、補集合\(\overline{A}\)と補集合\(\overline{B}\)は以下の領域になります。
ではこの補集合\(\overline{A}\)と補集合\(\overline{B}\)の共通領域(積集合)はどこかと考えると、、、↓ですよね!共通して赤色になっているのは集合A集合B両方の外側だけです!
\(\overline{A} \cap \overline{B}\)

そして、この領域は、、、上の\(A \cup B\)と真逆ですよね!つまり、これの補集合\(\overline{ A \cup B}\)と\(\overline{A} \cap \overline{B}\)は同一ということができます。
ですので、結局、↓が成り立つと言えるのです!
\( \large \overline{ A \cup B} = \overline{A} \cap \overline{B} \)
ド・モルガンの法則2の解説
次は法則2。これも同様にしていけば、式がなりたつことが言えます。
\( \large \overline{ A \cap B} = \overline{A} \cup \overline{B} \)
すなわち、積集合\(A \cap B\)の補集合は、実は保集合\(\overline{A}\)と補集合\(\overline{B}\)の和集合と同一なんです!これも絵でみていきます。
これに対して、補集合\(\overline{A}\)と補集合\(\overline{B}\)は先程の通りなので、その和集合だけ考えてみます。
\(\overline{A} \cup \overline{B}\)

そして、この絵は、、、上の\(A \cap B\)と真逆ですよね!つまり、これの補集合\(\overline{ A \cap B}\)と\(\overline{A} \cup \overline{B}\)は同一ということができます。
ですので、結局、再掲になりますが↓が成り立つと言えるのです!
\( \large \overline{ A \cap B} = \overline{A} \cup \overline{B} \)
ド・モルガンの法則の意味。補集合をとる時は\( \cup \)と\( \cap \)を逆にすればOK!
さて、ここまでで↓のド・モルガンの法則を解説/証明してきたド・モルガンの法則ですが、どういった意味があるのでしょうか。
[法則1]
\( \large \overline{ A \cup B} = \overline{A} \cap \overline{B} \)
[法則2]
\( \large \overline{ A \cap B} = \overline{A} \cup \overline{B} \)
この意味は「和集合や積集合の補集合を考える時は、その符号を逆にすれば分解できる」ということです。
法則1の\(\overline{ A \cup B}\)は和集合の補集合を考える、、、という意味です。そしてこれは、\(\overline{A} \cap \overline{B} \)に変換できます。
法則2の\(\overline{ A \cap B}\)は積集合の補集合を考える、、、という意味です。そしてこれは、\(\overline{A} \cup \overline{B} \)に変換できます。
つまり、補集合をとるときは、符号を逆にすれば分解できる!ということなんです。\( \cup \)があったら\( \cap \)にしてA,Bの補集合を合わせればいいし、\( \cup \)だったら\( \cap \)にしてA.Bの補集合を合わせれば良い。それだけの話です。
ド・モルガンの法則をシミュレーターを使って理解しよう!
それでは、ここまでド・モルガンの法則を実際にシミュレーションで体感してみましょう!
- A集合,B集合それぞれで、そのままの集合を選ぶか補集合を選ぶか選択できます
- さらに、演算子として\( \cup \)を選ぶか\( \cap \)を選ぶか選択できます
- 最終的にその組み合わせの式が↓に表示され、その式を示す領域が自動的に図示されます
色々選択変えてみて、1)選択した式がどのの領域になるのか確認、2)集合/演算子全て反対にすると真逆の領域が赤く塗られることを確認しましょう!
A集合
\(\large A\)
\(\large \overline{A}\)
B集合
\(\large B\)
\(\large \overline{B}\)
演算子
\(\large \cup \)
\(\large \cap \)
…
シミュレーション結果の解説
ド・モルガンの法則は簡単にいうと、集合A,Bも演算子\( \cup \)\( \cap \)も反対にすれば、補集合(逆の領域)を示すようになるって意味です!ですので例えば、
に対して全て逆のほうを選択すると
と真逆の領域(補集合)を指し示すことになります。不思議ですが、常にこれが成り立ちます!色々実験してみてくださいませー(*^_^*)
まとめ:ド・モルガンの法則を使うと、楽に補集合が求められる!
今回は集合の発展として、ド・モルガンの法則について解説しました!
ド・モルガンの法則は、和集合や積集合が組み合わさっている時に、楽に補集合をとるための法則です。基本は上記の通り、「集合/演算子含めて、全て逆にすれば良い」です。演算子\( \cup \)と\( \cap \)を逆にするというのがキーポイントです!
次回は集合から少し離れて、命題の基礎について解説していきます!命題は集合とは全く違うように思えますが、実は密接に関係しているんです!
- 和集合と積集合は、補集合をとると逆転する
- イメージ的には演算子\( \cup \)と\( \cap \)をひっくり返せばよい
⇒「集合と命題」カテゴリ記事一覧
その他関連カテゴリ