「補集合」の概念をシミュレーターを用いて解説！[数学入門]

2020-07-12　

本カテゴリでは数学の「集合」と「命題」について解説していきます。集合とは「何らかの条件にあてはまる要素の集合」です。そして「命題」とも深く関わりがあります。日常生活とも密接に関係のあるお話になりますので、集合の基礎イメージを理解しておきましょう！

今回は、前回の集合の基礎の話として、補集合の解説をしていきます！
「補集合」の概念をシミュレーターを用いて解説！[数学入門]

集合の基礎のおさらい

まずは集合の基礎についてのおさらいです。集合とは「何らかの条件に当てはまる要素を集めたもの」です。例えば、集合の例として以下のようなものがあります。

[集合の例]
「1以上10未満の整数」の集合：1,2,3,4,5,6,7,8,9
「空を飛べない鳥」の集合：ペンギン,ダチョウ,エミュー,ドードー,…
「\(x^2 < 4\)を満たす数」の集合：\(-2 < x < +2\)

こういったように、「なんらかの条件がついた1つの集合と、それにあてはまる複数の要素」という関係になっています。

この集合と要素の関係は、↓のように数学記号で以下のように表します。

[集合Aが要素xを含む場合]
全体集合U内の要素xを集合Aが含む場合、
\( \large x \in A \)
と表す。

また、逆に要素xが集合Aに含まれない場合は↓のように\( \notin \)記号で表します。

[集合Aが要素xを含まない場合]
全体集合U内の要素xを集合Aが含まない場合、
\( \large x \notin A \)
と表す。

それでは今回の主題の補集合の説明に入ります。補集合とは、簡単にいうと「集合Aに含まれない要素xのあつまり」です。簡単に言うと、「集合Aの反対」です！

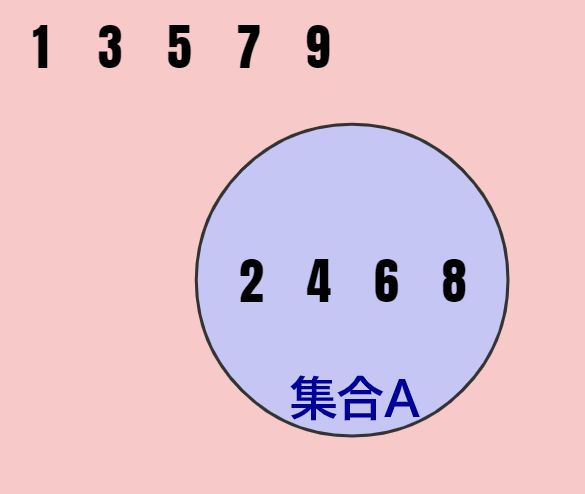
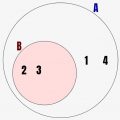
どういうことか、「偶数集合A」の例を用いて解説していきます。今、簡単のために全体集合U={1~9の自然数}という条件で考えていきます。そうすると、以下の青背景部分のように「偶数集合A」を定義できます。

このときに、枠外の赤い部分に「1,3,5,7,9」という数字がありますよね。これは偶数集合Aに含まれない数字の一覧です。そしてこれこそ、Aの補集合の要素なんです！

大事なのは全体集合Uの要素は「集合A」「Aの補集合」どちらかに入ることという事です。集合Aに入らなければ、補集合に入るはずですし、その逆も然り。つまり、

「集合A」+ 「Aの補集合」 = 全体集合U

が必ず成り立ちます！しかも重複する要素はないので、「集合A」「Aの補集合」で全体集合Uを2つに分割している感じになります。↑の図の通りですね！（青い領域集合Aと赤い領域Aの補集合の分けている）

↑で示した補集合、数学的な記号で定義すると以下のようになります。

補集合の定義

全体集合U内の以下の条件を満たす要素x
\( x \notin A \)
全てに対して、
\( x \in B \)
となる集合BをAの補集合といい、記号\(\bf \overline{A} \)で表す

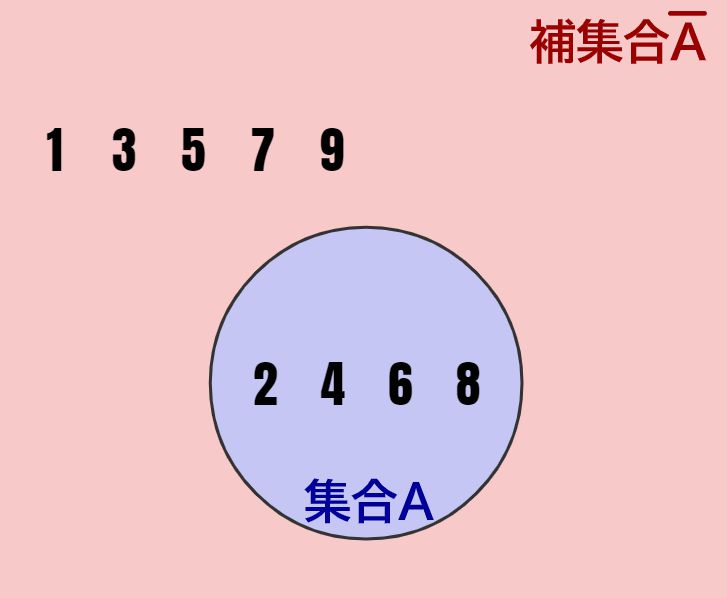
Aの補集合は、\(\bf \overline{A} \)という上に線を引いた記号で表すルールとなっています！つまり、この記号を用いて先程の集合と補集合の図を表すと以下のように表せます。赤い領域は\(\bf \overline{A} \)の集合と言えるわけです！

POINTAの補集合 = 集合Aに含まれない要素xのあつまり。集合Aの反対といえる！

ここで補集合の概念のイメージをつけるために、シミュレーターで確認してみましょう！

シミュレーションの説明

集合Aの要素選択
1 2 3 4 5 6 7 8 9

今回は前回の発展として補集合について解説しました！結局、補集合\(\bf \overline{A} \)は集合Aの反対を表す集合で、Aに入らないものを集めた集合です。簡単ですが、超重要な基礎ですので↑のシミュレーターでイメージを確実につかんで頂けたらと思います！
　

まとめ

　
次回は集合の概念の中で大事な、「部分集合」についてシミュレーターを用いて解説していきます！

[関連記事] 数学入門：集合と命題

2．補集合(本記事)