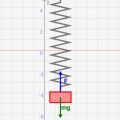
バネ運動時のエネルギー保存則をシミュレーションで理解しよう![物理入門]
前回までの記事で、バネによってどのような力が発生するかの解説をしました。
今回はそのバネによる運動時のエネルギー保存則について考えていきます!
![バネ運動時のエネルギー保存則をシミュレーションで理解しよう![物理入門]](https://retu27.com/wp-content/uploads/rapture_20210520202637-500x320.jpg)
目次
おさらい:バネによる力の法則
まずはおさらいです。バネの力は↓のような力が働きます。
バネによる力 \(F = -kx\)
- k : バネ定数
- x : バネの自然長からの変位[\(m\)]
↓バネからの変位によって縮まる力・押す力が決まります。
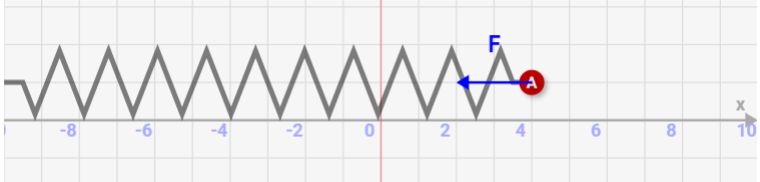
↓自然長からの変位が2倍になると、力が2倍になります。これがバネによって働く力なんです!
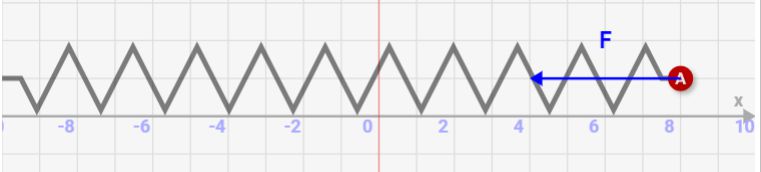
バネ運動時のエネルギー保存則
上記のような力が発生する場合にどのようなエネルギー保存則が成り立つか考えていきます。
今、運動エネルギーを\(U_v\)、バネによるエネルギーを\(U_e\)と出来るなら、↓のような関係がみたせるはずです。
\( \displaystyle U_v + U_e = 不変 \)
↓微分
\( \displaystyle ⊿U_v + ⊿U_e = 0 \)
↓変形
\( \displaystyle ⊿U_v = – ⊿U_e \)
つまり、運動エネルギーの運動前後の変化が、バネエネルギーの増減と逆になるはず。
そして、コチラのページで解説している通り、運動エネルギーU_v=\(\frac{1}{2}mv^2\)の変化はかかった力Fをxで積分した値と等しいです。
\( \displaystyle ⊿U_v = \int F dx \)
つまり、バネエネルギーは↓のように、「バネによる力F」をxで積分してマイナスすれば求められるはずなんです!
\( \displaystyle ⊿U_e = - \int バネによる力F dx \)
これにF=kxを代入すれば、↓のように求められ、
\( \displaystyle ⊿U_e = - \int F dx \)
↓バネの力F=-kxを代入
\( \displaystyle = \int kx \ dx \)
さらにこれを積分すれば、バネ定数k、自然長からの距離xのバネのエネルギーは↓となります。これをバネによる弾性エネルギーと呼びます!
\( \displaystyle U_e= \frac{1}{2}kx^2 \)
- k : バネ定数
- x : バネの自然長からの変位[\(m\)]
シミュレーターで「バネによるエネルギーの保存則」を確認しよう!
それでは上で説明した「バネによる弾性エネルギー」の保存則をシミュレーターで実際に確認しましょう!
- スライドバーによって変位x,バネ定数k,物体の質量mが変えられます
- 指定した設定を初期値として、物体がバネの力で振動を開始します
- 同時にバネによる弾性エネルギーと運動エネルギーをグラフに図示します
- エネルギー全体が変わらず、保存則が成り立つことを確認しましょう
- エネルギー総量がバネ定数に比例し、変位xの二乗に比例することを確認しましょう
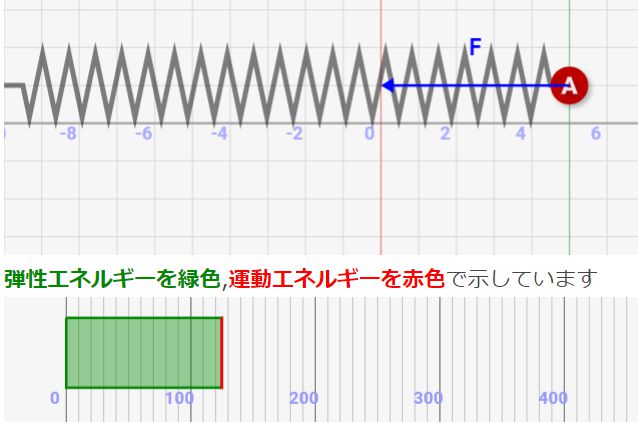
弾性エネルギーを緑色,運動エネルギーを赤色で示しています
シミュレーター結果の解説
シミュレーターで↓のようなことがわかると思います。
バネ振動の両端では全てバネ弾性エネルギーとなる
バネの両端では物体が一時的に停止するので速度v=0となり、全て弾性エネルギーに変わります。
振動の中心(自然長)では、全て運動エネルギーに変わる
上記の端とは逆で、物体が真ん中にくると弾性エネルギーはx=0なので0になります。その分、運動エネルギーが最大になるわけです。

バネ振動で、弾性エネルギーと運動エネルギーの変換が繰り返される
バネ振動では上記の2パターンを永遠と繰り返すような動作になります。「弾性エネルギー→運動エネルギー→弾性エネルギー…」と繰り返します。
摩擦がない限り、このように永遠とエネルギーの変換を繰り返し続けるんですね!

次回は、位置エネルギーも含めた3種のエネルギー保存則について考えてみたいと思います!
- バネ振動では弾性エネルギーと運動エネルギーが交互に変換され続ける
- エネルギーの総量は変わらず、エネルギー保存則が成り立つ
⇒「単振動(バネ運動)」カテゴリ記事一覧
⇒「運動エネルギー」カテゴリ記事一覧
その他関連カテゴリ