「命題の否定(論理和/論理積/全称命題/存在命題の否定)」を、図式を用いて解説![数学入門]
本記事では数学の「命題の否定」について解説していきます。前回まで数学の集合に関する説明をシミュレーターを用いてしてきました。本記事からは、その考えを応用して「命題」について解説していきます!
命題は、日常的にも出てくる概念です。そして間違った知識でこの命題を扱うと、論理的に間違った結論が出てしまったりします><ですので、数学関係なくとも命題に関する正しい知識を身に着けておきましょう!
前回記事で、「各命題/条件の真偽」は実はその「対偶命題/条件の真偽」とイコールになるということを解説しました。そして、その待遇をとるためには、命題/条件の否定をとる必要があります。
そこで今回の記事は論理和/論理積/全称命題/存在命題といった表記に対する、否定のとり方を考えていきます!基本は集合的に考えれば良いので、集合的に「補集合をとる」ことを考えていけばOKです!
![「命題の否定(論理和/論理積/全称命題/存在命題の否定)」を、図式を用いて解説![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200712205828-500x454.jpg)
目次
命題/条件の論理和/論理積とその否定
論理和/論理積とは
まずは論理和/論理積の説明です。論理和/論理積とは以下のような命題/条件をいいます。
論理積:AかつB (AとB両方が真のとき、真となる)
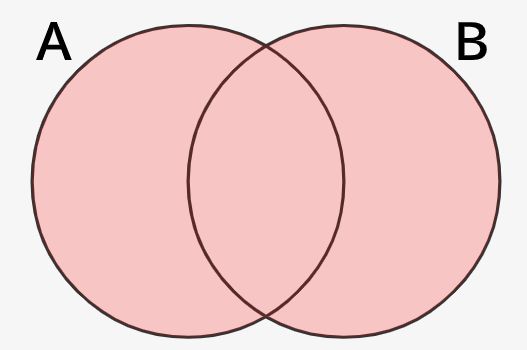
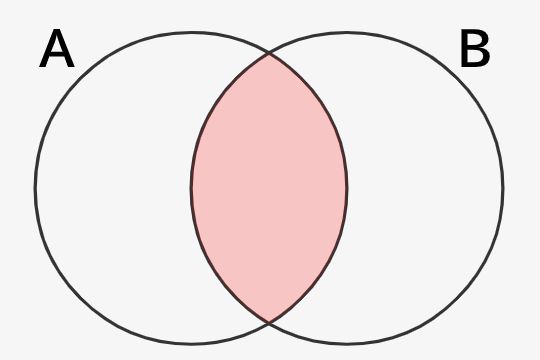
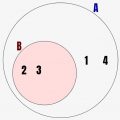
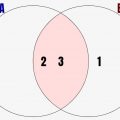
という感じです。集合的にいうと、↓のような感じです。
これ、まさしく集合のところで解説した和集合と積集合と同一なんです!
つまり、論理和/論理積をとることで、集合的にみると論理和ならA,Bの領域を合体した部分となり、論理積ならA,Bの共通部分が演算後の集合になるんです!
簡単な例をあげると、
A: 鳥
B: 飛べる
として、
論理積:鳥 かつ 飛べるもの
となります!簡単ですね。
論理和/論理積の否定
さて、上の式の否定を考えます。対偶をとるためには、否定を考えなければいけないのです。
で、ここで出てくるのがまた集合論で解説した、ド・モルガンの法則です!
[法則1]
\( \large \overline{ A \cup B} = \overline{A} \cap \overline{B} \)
[法則2]
\( \large \overline{ A \cap B} = \overline{A} \cup \overline{B} \)
結局、命題も集合として見られるため、この法則が使えます。ですので、命題/条件A,Bの論理和/論理積の否定は以下のようになります。
論理積:\(\overline{A}\) または \(\overline{B}\)
まさしく、上記のド・モルガンの法則通りです。簡単ですね!
全称命題/存在命題とそのの否定
次に全称命題/存在命題について考えていきます
全称命題/存在命題とは
まず全称命題/存在命題の説明です。全称命題/存在命題とは以下のような命題のことを言います。
存在命題:あるxに対して命題Aが成り立つ
簡単にいうと、全称命題は与えられた仮定集合に入る全てのxで命題が成り立つことを示さないといけないです。
それに対して、存在命題は、一つでも命題Aがなりたつxが見つかればこの命題が成立するんですね!存在命題のほうが示すのが圧倒的に簡単そうですね(*^_^*)
では、実例を見てみましょう!
全称命題/存在命題の例
存在命題:ある鳥は、空を飛べる
こんな感じです。絵にすると、↓のような感じです
全称命題の例
鳥集合の中全て空をチェック飛べるか確認しないと真と言えない
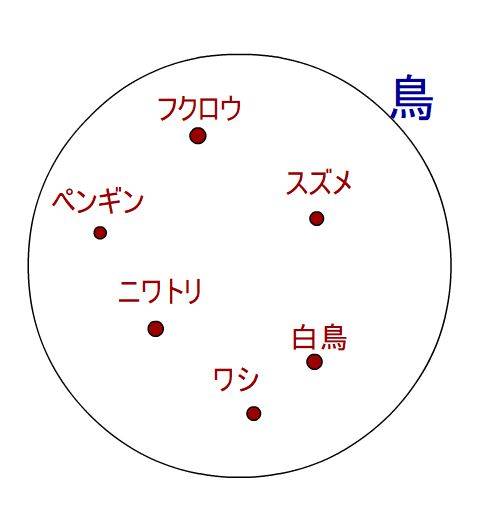
存在命題の例
鳥集合の中全て空を飛べるものを1つでも見つければOK
これが全称命題と存在命題の違いです。存在命令は一種でも確認できればいいので、簡単に示せるんですね。
全称命題/存在命題の否定
上記で説明した全称命題/存在命題の否定について解説します。結論としては、↓の通りになります。
存在命題の否定:全ての(任意の)xに対して命題Aが成リ立たない
つまり、全証命題の否定は存在命題になり、存在命題の否定は全称命題になるんです!!
絵と例で考えると、とても分かりやすいです。
全称命題:全ての鳥が、空を飛べる
→全証命題の否定:ある鳥が、空を飛べない
存在命題:ある鳥は、空を飛べる
→存在命題の否定:全ての鳥が、空を飛べない
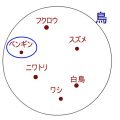
全証命題の否定の例
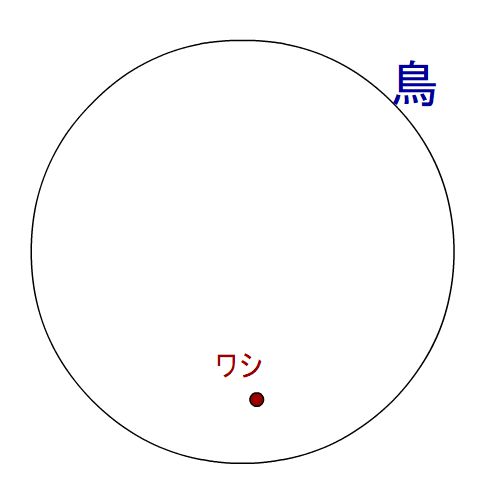
全称命題「全ての鳥が、空を飛べる」といっている人に反論するためには、一匹でも空を飛べない鳥を見つけて提示すればOKです。「存在命題:ある鳥は、空を飛べる」が成立します。ですので、↓の図のようにペンギンを見つけてきて提示すればOKなんです。
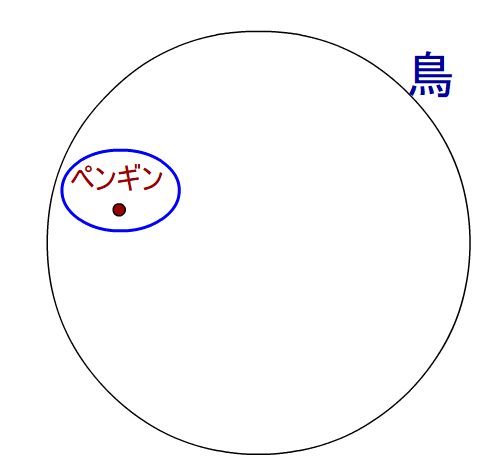
存在命題の否定の例
存在命題「ある鳥は、空を飛べる」を証明するのは大変です。これを否定するためには、↓の図の例のように「全ての鳥が、空を飛べない」を証明しないといけません。つまり、全ての鳥を調査して否定する必要があるんですね。全称命題を否定するよりも圧倒的に大変ですね><
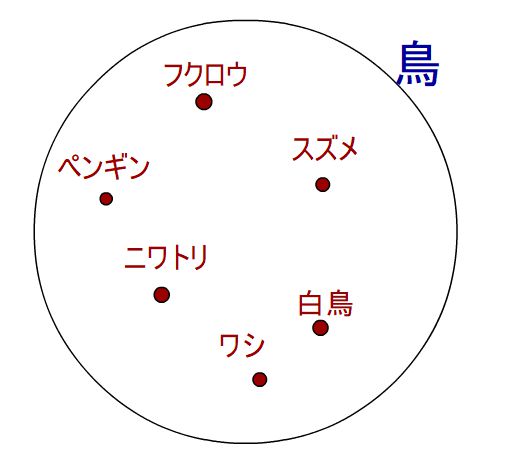
まとめ:論理和/論理積/全称命題/存在命題の否定はそれぞれ逆の演算子になる!
最後にまとめです。今回は命題の論理和/論理積/全称命題/存在命題について説明し、その否定のとり方について説明しました。
論理和/論理積は集合の和集合/積集合そのものであり、ド・モルガンの法則通りに否定を行えばOKです。否定すると論理和は論理積になり、論理積は論理和になります。
全称命題/存在命題はその意味を考えていけばOKです。全称命題は「全てのxに対してAがなりたつ」というもので、存在命題は「あるxでAがなりたつ」というような命題です。
これの否定をとると、全称命題は存在命題に、存在命題は全称命題になります。
ときどき、この辺りの否定の仕方を間違えて、「全ての鳥は、空を飛べる」の否定が「全ての鳥は、空を飛べない」だと勘違いしている人がいます。そうならないように、ちゃんと意味を考えて命題の否定をとるようにしましょう!
- 命題には論理和/論理積があり、その否定をとると記号が逆転する(ド・モルガンの定理と同じ)
- 命題には全称命題/存在命題もあるが、こちらも同様に否定をとると両方逆転する
- ともに記号が反対になるのを意識すれば、否定命題も分解して解くことができるh
次回はこの否定を使った、数学の証明方法「背理法」について説明していきます!!
⇒「集合と命題」カテゴリ記事一覧
その他関連カテゴリ