数学入門:命題の基礎(命題/集合との関係/必要条件と十分条件)を、図式を用いて解説!
本記事から数学の「命題」について解説していきます。前回の記事まで数学の集合に関する説明をシミュレーターを用いてしてきました。本記事からは、その考えを応用して「命題」について解説していきます!
命題は、日常的にも出てくる概念です。そして間違った知識でこの命題を扱うと、論理的に間違った結論が出てしまったりします><ですので、数学関係なくとも命題に関する正しい知識を身に着けておきましょう!
本サイトでは図式やシミュレーターを用いて「命題」を分かりやすく解説していきます!シミュレーターで実験して、命題の意味を深く理解して頂ければと思います!
目次
命題とは?
まず命題とは何かですが、一般的な定義は以下の通りです。
「正しい(真)」か「正しくない(偽)」か明確に客観的に決められる文や式
ということです。正しいか正しくないか決められたらそれは命題なのです。分かりやすいように具体的な例を挙げていきます!
全ての鳥は空を飛べる
愛知県は日本一人口が多い県である
1+1 = 2
奇数は自然数である
\(x^2 < 4\)ならば\( -2 < x \)である
このように、真(正しい)か偽(正しくない)か決められるのが命題です。最初の「全ての鳥は空を飛べる」は偽ですよね。ペンギンなどがいるので。その真偽は置いておいて、このように正しいか正しくないか客観的に答えられるのが命題です。逆にいうと「ペンギンはかわいい」というのは命題になりません。人によって主観によって真偽が変わるからです><
その他も全て命題です。ものによって、数字が出たり出なかったりしますが、とりあえず全て客観的に真偽が答えられるので全て命題と言えます!
命題は「\(p \Rightarrow(ならば) q\)」という形で表すと、集合論に考えられる!
上記のように命題がある中で、実は多くのものが「p ならば q」という形で表せます。これを数学では「\(p \Rightarrow q\)」という形で表します。\(\Rightarrow\)が「ならば」という意味ですね。
例えば、↑の命題の例は以下のような\(\Rightarrow\)を使った形式で表せます。
鳥 \(\Rightarrow\) 空を飛べる
愛知県 \(\Rightarrow\) 日本一人口が多い県
奇数 \(\Rightarrow\) 自然数
\(x^2 < 4\) \(\Rightarrow\) \( -2 < x \)
命題「1+1 = 2」などこの形式に直せない命題ものもありますが、多くの場合はこのような「ならば\(\Rightarrow\)」を使った形式で表せることが多いです。
そして、このような形式に変換すると、「今までやった集合的な考えで命題の判定ができる」ようになるのです!
「\(p \Rightarrow(ならば) q\)」と表せるとき、pを仮定、qを結論と呼びます。以下、この呼び方で説明していきます。
命題「\(p \Rightarrow(ならば) q\)」を集合論的にあらわしてみよう!
それでは↑で変換した「\(p \Rightarrow(ならば) q\)」という形式の命題を集合的な図で表してみましょう!
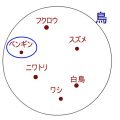
命題「鳥 \(\Rightarrow\) 空を飛べる」は↓のような図になります。「鳥」という集合と、「飛べるもの」という集合があり、それぞれ微妙にズレています。

これを要素含めて書くと、↓のようになります。「鳥」の要素としては「すずめ、ワシ、ペンギン」などがいます。もちろん、鳥はもっともっといますが、省略して書いてます。そして、それとは別に「飛べるもの」集合があり、「すずめ、ワシ」はその集合にも入っています。しかし、「ペンギン」は「飛べるもの」集合に入っていません。飛べないですからね。

この例では、「鳥」だけど「飛べるもの」に入らない「ペンギン」がいるので、この命題「鳥 \(\Rightarrow\) 空を飛べる」は偽になるわけですね。では、どのような場合に命題は真となるんでしょうか。
命題「\(p \Rightarrow q\)」は、仮定pが結論qの部分集合(完全包含)しているときだけ真といえる!
上記の鳥の例では、「鳥だけど飛べないペンギン」がいることで命題が偽になっていました。では、どんな時に「\(p \Rightarrow(ならば) q\)」が成り立つかと言うと、、、「結論qが仮定pを包含する時」「仮定pが結論qの部分集合となるとき」なんです!
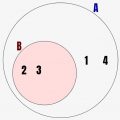
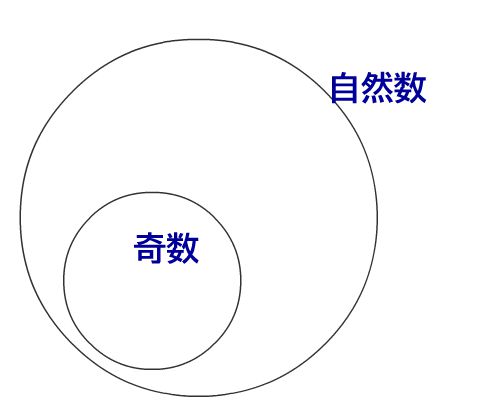
それを示すのが命題「奇数 \(\Rightarrow\) 自然数」です。これを図示すると↓のようになります。奇数は1,3,5,7,9… であり、すべて自然数です。自然数が奇数を包含しているため、図にすると↓のようになります。
命題が真となるのは、「仮定p集合の全ての要素xについて、結論集合qに属する時」です。数式で書くと
\( x \in p \)
を満たすx全てに対して、
\( x \in q \)
となる
ですね。これって実は見たことある条件なんです。そう、部分集合の定義と全く同じなんです!
つまり、
なんですね!
命題「\(p \Rightarrow q\)」の必要条件/十分条件の関係
上記の説明の通り、実は命題「\(p \Rightarrow q\)」は集合関係\(p \subset q \)を示すことと同値です。
そして、この命題が成り立つ時、以下のような言葉でp,qを表します。
「pはqであるための十分条件」
「qはpであるための必要条件」
という
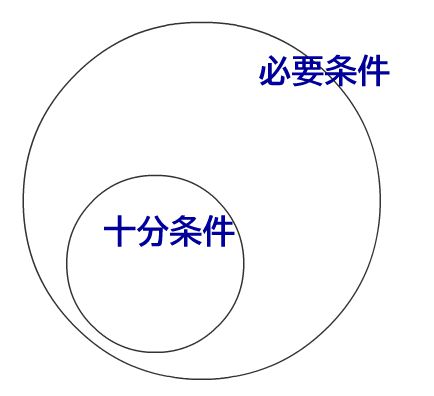
非常にややこしいですが、「仮定pを十分条件」「結論qを必要条件」と言います。集合論的に考えると、以下の図のように表せます。
\(仮定p \subset 結論q \)のときにこの命題が成り立つので、↑のような関係になっているとき、小さいほうの集合を十分条件、大きい方の集合が必要条件になります。
あまりにも言葉がわかりにくいので説明しておくと、、
必要条件:この集合の条件を満たすことが、集合pに入るために必要な条件(この集合に入っていない限り、集合pに入ることは不可能)
という意味合いです。
命題の逆「\(q \Rightarrow p\)」を考える
今まで命題「\(p \Rightarrow q\)」について考えてきましたが、ここで命題の逆「\(q \Rightarrow p\)」を考えます。もしも、「\(q \Rightarrow p\)」も成立していた場合、それはどんな時なんでしょうか。
結論からいうと、命題「\(p \Rightarrow q\)」と命題の逆「\(q \Rightarrow p\)」が成り立つのは集合p = 集合qのときだけです。
なぜならば、「\(p \Rightarrow q\)」なら\(p \subset q \)であり、「\(q \Rightarrow p\)」なら\(q \subset p \)だからです。この2つを満たすのは、pとqが全く同じ集合の場合、つまりp=qの場合だけです!
そして、このp=qが成り立つ時、
「pはqであるための必要十分条件」
「qはpであるための必要十分条件」
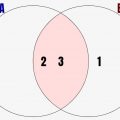
といいます。それは、p,q互いに十分条件でもあり必要条件にもなっているからです。図にすると↓のような感じ。集合pとqが完全一致した時だけ、必要十分条件となります。
まとめ:命題は集合論的に評価できる!
最後にまとめです。今回は数学の命題について説明してきました。命題とは「正しい(真)」か「正しくない(偽)」か明確に客観的に決められる文や式です。その中でも、\(p \Rightarrow(ならば) q\)という形で表せる命題は多く、それらは集合論的に考える事ができます!
結論としては、\(p \Rightarrow q\)ならば\(p \subset q\)が成り立ちます。つまり、命題の真偽の判定はpとqが部分集合か否かという論議に代えられます。そして、\(p \subset q\)が成り立つとき、「pは十分条件」「qは必要条件」と呼ぶことができます。↓のような大小関係になっていることを頭に入れておいてくださいませ!
- \(p \Rightarrow q\)という命題は、実は\(p \subset q\)が成り立つことと同等
- 命題を証明するためには、pがqの部分集合であることを示せば良い
次回はこのような命題の「逆/裏/対偶」について解説していきます!
⇒「集合と命題」カテゴリ記事一覧
その他関連カテゴリ