集合の基礎(集合/全体集合/空集合)をシミュレーターを用いて解説![数学入門]
本記事から数学の「集合」と「命題」について解説していきます。集合とは「何らかの条件にあてはまる要素の集合」です。そして「命題」とも深く関わりがあります。日常生活とも密接に関係のあるお話になりますので、集合の基礎イメージを理解しておきましょう!
シミュレーターで実験して、その概念を深く理解して頂ければと思います!
![集合の基礎(集合/全体集合/空集合)をシミュレーターを用いて解説![数学入門]](https://retu27.com/wp-content/uploads/rapture_20200711144010_2-500x456.jpg)
目次
集合とは
集合とは「要素の集まり」です。特に数学では「何らかの条件に当てはまる要素を集めたもの」が集合になります。言葉だけだと非常に分かりにくいので例で考えてみましょう!
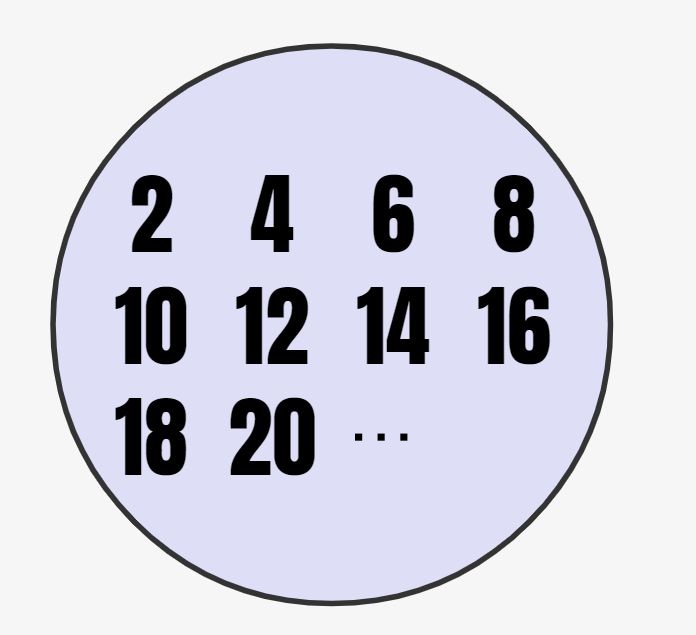
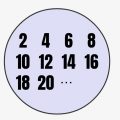
↓は「偶数」という条件に当てはまる集合の例です!
青背景の中にあるのが要素で、枠がこの集合を表しています。枠内を見ると、「2,4,6,8,…」と偶数の数字が集まっていますよね。これがそれぞれ要素です。このように特定の条件を満たすものを「集合」といいます。
集合の例をみていこう!
集合のイメージをつけるために、いくつかの集合の例を見ていきましょう!集合は数字だけの話ではないのです!
「1以上10未満の整数」の集合:1,2,3,4,5,6,7,8,9
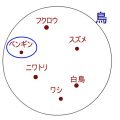
「空を飛べない鳥」の集合:ペンギン,ダチョウ,エミュー,ドードー,…
「アジアの国」の集合:日本,韓国,中国,モンゴル,…
「\(x^2 < 4\)を満たす数」の集合:\(-2 < x < +2\)
↑の例のように、集合は数字だけのものでは有りません。「飛べない鳥」「アジアの国」など、言葉や概念の集合もあります。もちろん、「1以上10未満の整数」といったような数学的な集合もあります。
注意すべきは「\(x^2 < 4\)を満たす数」です。これは\(-2 < x < +2\)が要素になりますが、、、-2~+2内の実数全てが当てはまることになります。例えば、1.117とか-0.29とか。無限にあるわけで。つまり、要素が数えられるとは限らない場合もあるのです!
補足:集合には「無限集合」「有限集合」がある!
これは補足になりますが、集合には「無限集合」「有限集合」があります。↑の「偶数全体」の例は無限集合です。なぜなら、偶数は無限にあるからです。無限集合は要素の数が決められないのです。例えば、222222…とか。それに対して、「1以上10未満の整数」「アジアの国」等は有限集合ですよね。必ず数は決まっており、要素数を決定できるはずなので(*^^*)
また、「\(x^2 < 4\)を満たす数」も無限集合ですよね。要素数が決まらないので。完全に補足になりますが、実は「偶数全体」と「\(x^2 < 4\)を満たす数」は本当はレベルが違います。ここでは詳しくは述べませんが、自然数での無限と実数での無限でレベルの差があるのです>< (可算無限と非可算無限)
全体集合とは
もう一つ、大事な概念「全体集合」の説明を先にしておきます。全体集合とは「考えている考えている対象全体」のことです。分かりにくいので例を見てみましょう!
全体集合「自然数」:1,2,3,4,5,6,7,8,9,10,…
全体集合「鳥」:スズメ、ペンギン,ニワトリ,フクロウ…
全体集合「動物」:人間,スズメ,シャチ,マグロ,…
全体集合「1以上10未満の自然数」:1,2,3,4,5,6,7,8,9
こんな感じです。基本的には、全体集合も集合の一種であり、考え方は同じです。有限集合のときもあるし、無限集合のときもあります。
ただ、全体集合を決めることで、考えている範囲をちゃんと定義するってことが重要なんですね!例えば、「飛べない鳥」の集合を考えているときでも、「鳥」を全体集合にとるか、「動物」を全体集合ととるかで考え方が変わってくるので(*^_^*)
全体集合は
といったように、Uという記号で表される事が多いです。
集合記号を理解しよう!
ここで、全体集合U内の要素xと集合Aの関係を示す数学記号の説明をしておきます!
全体集合U内の要素xを集合Aが含む場合、
\( \large x \in A \)
と表す。
全体集合U内の要素xを集合Aが含まない場合、
\( \large x \notin A \)
と表す。
全体集合U内の要素xは集合Aに含まれるか、もしくは含まれないかのどちらかです。ですので、要素xが集合Aに含む場合\( x \in A \)と表し、含まない場合は\( x \notin A \)と表すというルールです。
偶数の例であれば、以下の例のように表せます。
\( 2,4,6,8,… \in 偶数集合A \)
\( 1,3,5,7,… \notin 偶数集合A \)
以後、この表記で要素と集合の関係を表していきます!
「nの倍数の集合」シミュレーターで「集合」を理解しよう!
ここで集合の概念のイメージをつけるためにシミュレーターで確認してみましょう!
- このシミュレーターでは「自然数nの倍数」の集合を表示します
- スライドバーで自然数nを変えて、集合が変わることを確認しましょう
- 分かりやすくするため、全体集合U={1 ~ 20}の範囲で表示するようにしています
「空集合」の概念を理解しておこう!
上記のシミュレーターですが、基本的には指定したnの倍数が表示されますよね。
しかし、n=0を指定すると
というように、一つも要素がない集合になってしまいます。0の倍数なんて、無いですからね。実は、これも集合の一つであり、空集合といいます。空集合の定義は以下の通りです!
全体集合U内の任意の要素xに対して、
\( x \notin A \)
となる集合A
前述の通り、\( \notin \)はその集合に属さないことを表す記号です。つまり、要素が一つもない場合、空集合になるんですね。空集合は
という記号で表します!空集合はすごく重要な概念なので理解しておきましょう!
まとめ:集合=何かしらの条件にあてはまる要素の集まり
今回は数学の集合の基礎的な概念の説明をしました!少し長くなりましたが、わかれば簡単ですよね!「集合=何かしらの条件にあてはまる要素の集まり」です。これさえ理解しておけば大丈夫です!
次回、集合の概念の中で大事な「補集合」についてシミュレーターを用いて解説していきます!
- 集合 = 「何かしらの条件を満たす要素の集まり」
- 全体集合 = 考えている領域全ての要素を集めた集合
- 空集合 = 要素が1つもない集合
⇒「集合と命題」カテゴリ記事一覧
その他関連カテゴリ