運動量保存の法則をシミュレーションで解説！運動エネルギーが保存される条件もわかります！[物理入門]

2020-03-19　 運動量

新しいコンテンツとして物理学や数学/統計学などをシミュレーションで解説していきます。今現在でも、物理学など解説してくれているサイトはあるのですが、動きがわからず、実際に動かしたりできないので少しわかりにくい面があります。さらにシミュレーションソフトなどもありますが、windowsの特定の環境でしか動かなかったりして、使いにくいです。

そこでこのブログでは、スマホでもPCでもどこでも動かせるようなシミュレーションを用いることで、わかりやすく物理や数学を理解できるようなコンテンツを増やしていきます！今回は、前回に引き続いて運動物理学の解説です。前回の反発係数の説明を発展させて、運動量保存則について説明していきます。

運動量保存の法則をシミュレーションで理解！

それでは、ボールの衝突をシミュレーションできるツールを掲載します。使い方は簡単、下記の速度や質量の数値を変えて実行を押してみて下さい！「A」「B」と書いてあるのがボールです。実行ボタンを押すと衝突が起こり、運動量や運動エネルギー(後述)を計算してくれます。
* 速度をマイナス指定することも可能です。その場合、左へボールが移動していきます。

運動量とは何か

運動量は下記のように定義できます。

これは、全ての物体の（質量×速度）の合計という意味です。少しわかりにくいので、今回のシミュレーターを例にすると、、、

のことです。登場する物体がAとBだけなので、この式になります。
　

運動量は何があっても変わらない

　運動量保存の法則とは「この運動量が何があっても不変」という法則です。何があってもというのは、衝突があっても保存されるということ。なので、もっと簡単に言うと

がなりたちます。さらに少しだけ式を変形させると。

です。これは、「Aの失った運動量＝Bが得た運動量」であることを意味します。シミュレーションでは数の例のように、Aの損失運動量が、Bの得た量と一致しているのがわかりますよね。どんなに値を変えてもこの「運動量保存の法則」は変わりません。これは、運動量を変化させる「力積」というものを考えれば当たり前のことなのですが、、、それはまた次回解説します。

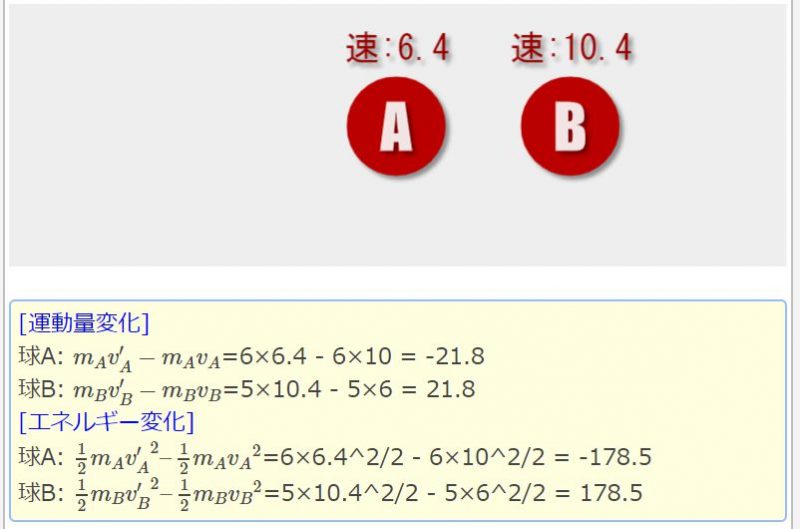
[シミュレーションの一例。運動量の変化はAとBで一致(-1倍)となる]

　

運動エネルギーは「反発係数=1」のときのみ保存される！

それでは、上記の例で運動エネルギーというものはどうなるのかを考えます。定義は以下の通りです(詳しくは運動エネルギーのページ参照)。

この運動エネルギーについて、詳しくは述べませんが、シミュレーションにおいて、「反発係数=1」のときのみ運動量が保存されます。発係数は前回の記事でも説明しましたが、ボール間で拡張した定義にすると、下記のような式で示せます。

これは、反発係数は「BとAの相対速度」の衝突前と衝突後の比率が反発係数になるという意味です。マイナス記号に注意です。さらに反発係数=1の場合には、下記のように式を変形できます。

　
これは、反発係数=1の場合は相対速度が全く変わらない(マイナスなので正確には逆転)ということを示しています。そしてこの場合に運動エネルギーが保存されます。証明はしませんが、これは重要な事実です。実際、上記のシミュレーションで反発係数を1で実行してみてください。必ず運動エネルギーの変動がAとBで一致するはずです。

運動エネルギーが保存されるということは、衝突の音エネルギーも熱エネルギーも発生しないということを意味します。現実世界では、そのような完璧にエネルギーを保存できる環境は少ないと思います。

[シミュレーションの一例。反発係数が1のときにのみ、運動エネルギーも保存される]

　

物理学シミュレーター記事集！

1．反発係数

2．運動量保存の法則(本記事)

3．力積と瞬間的な加速度運動