力積とは何か？瞬間的な加速度運動をシミュレーションで分かりやすく解説！[物理入門]

2021-05-05　 運動量

以前の記事で運動量保存則について説明しました。この運動量保存則は閉じられた系で成り立ちますが、それぞれの物体は速度が変わるごとに運動量が変化します。

今回はこの運動量を変化させる「力積」について詳しく解説していきます！

力積＝運動量mvの変化量

いきなりですが、質量m速度vで表せる運動量mvの速度が\(v_{変化前}\)から\(v_{変化後}\)に変化した時、運動量の変化量は↓の式で表せます。

右辺は運動量mvの変化量に相当します。基本的に物体の質量mは固定なので、m(v_{変化後} – v_{変化前})が運動量の変化量です。

それに対して、右辺は力Fに力をかけた時間⊿tをかけ合わせたものです。これを物理では力積と呼びます。力積は運動量の変化量と一致します。

なぜなら、速度の変化量\((v_{変化後} – v_{変化前})\)は加速度aに⊿tを乗算した値と一致するはず。さらに運動の第2法則から\(a=\frac{F}{m}\)となるはずなので、これを代入すると、、、

と変形できるからです。つまり、運動量の変化量は力積F⊿tと一致するんです！

時間tと力Fの面積が、運動量変化と一致する

上記のように運動量の変化量は力積F⊿tと一致します。この力積ですが、時間tを横軸、力Fを縦軸に描いたとき、その面積と一致します。

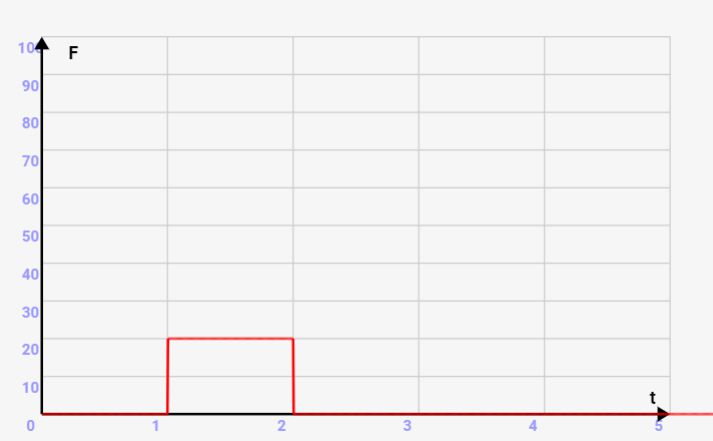
例えば↓は時間t=1~3の2秒の間に、力F=10Nがかかった事をしめしています。このとき、力積は2×10=20となります。これは↓のグラフの赤線で囲まれた領域の面積と同値となります。これは力Fが時間ごとで変化した場合も同じです。面積の領域が力積となります。

　

運動量の変化は同じなら、力Fと力がかかる時間⊿tは反比例する

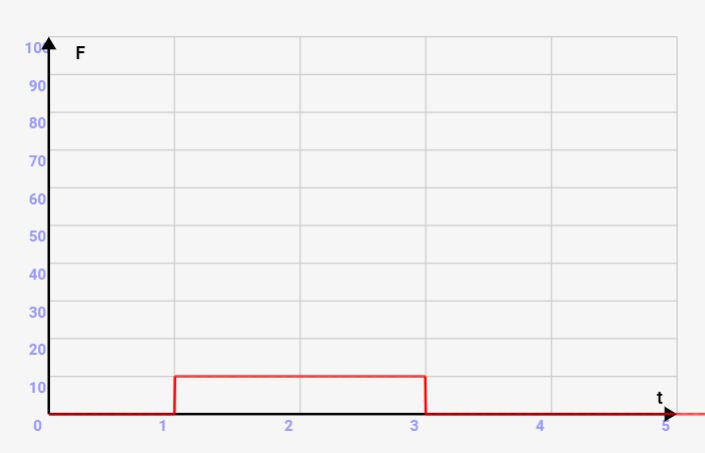
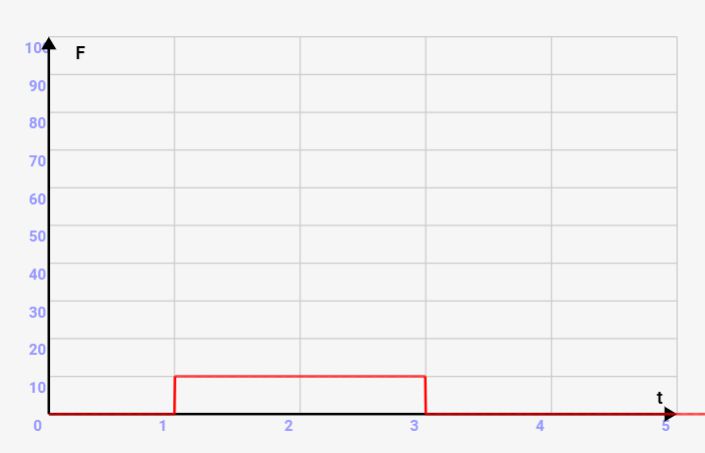
ここで、例として質量m=1で、速度vが10から30に変化したとします。このとき、運動量の変化量＝力積は20かかったはずです。

でも、同じ力積20でも、1秒で20Nかかる場合もあるし、

2秒で20Nかかる場合もあるはずです。

もしくは短期的に0.2秒で力がかかった場合、その力は100Nと強い力がかかるはずなんです。

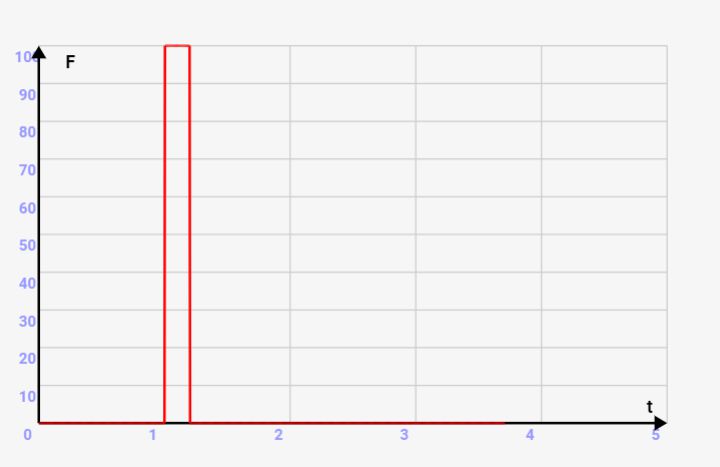
このように、同じ運動量の変化量＝20でも様々なパターンがあります。ただ、力Fとが一定にかかるならば、力Fと力がかかる時間⊿tには以下の関係が成り立ちます。これは運動量の変化量が一定⇒力積が一定なので自明な事実です。

つまり、力Fと⊿tは乗算すると一定の値になるはずであり、反比例の関係になるはずなんです！かかる時間⊿tが短いほど、かかる力Fは強くなります。短い時間で速度vを変化させなきゃいけないんですから、当たり前です。
　

シミュレーターで力Fと⊿tの関係を理解しよう！

上記の力積の考え方と、力Fのとかかる時間⊿tの反比例することを実際にシミュレーターで確認してみましょう！

↓反発時間をスライドバーで変えると、シミュレーターが動き出します。
力Fと反発時間⊿tが反比例になり、乗算すると20になることを確認しましょう！

まとめ：運動量変化は同じでも、力のかかり方は様々

最後にまとめです。以前説明した運動量保存則に対して、どのような要因で運動量に変化がおきるのかを今回は考えてみました。その変化を起こす要因こそ力積F⊿tです。力積と運動量の変化量は↓の通り、一致します。

物体が壁などにぶつかる時、その速度の変化が瞬時に起きます。壁にボールがぶつかると、反発係数の比の速度で押し返されます。この時に特別な変化が起きたように思えてしまいますが、、、瞬時に大きな力Fがかかり、通常の加速度運動と同じような速度の変化が起きているんです！

壁や地面への衝突で、加速度運動が起きているとイメージが湧きにくいですが、、、↑のシミュレーターのように、瞬間的に大きな加速度運動が発生しているんですね！
　

物理学シミュレーター記事集！

1．反発係数

2．運動量保存の法則

3．力積と瞬間的な加速度運動(本記事)