微分とは何か?「接線」と「その傾き」で定義を理解しよう![数学入門]
本記事から高校数学で一番重要と言える「微分」の考え方について説明します。微分は非常に分かりにくいものというイメージがあるかもしれませんが、その根本の意味を理解すれば、そこまで難しいものでは有りません。
ただ公式を覚えるだけでなく、その意味やイメージを理解することがすごく重要なんです!
![微分とは何か?「接線」と「その傾き」で定義を理解しよう![数学入門]](https://retu27.com/wp-content/uploads/rapture_20210422185024-500x433.jpg)
目次
微分の前に「平均変化率」「傾き」を理解しよう!
平均変化率の考え方
まず微分の説明の前に、「平均変化率」「傾き」について説明します。数学では「平均変化率」という考え方があります。これは「xが1増えた時にyはどれだけ増加するか」を表す値です。例えば、(x1,y1)から(x2,y2)に移動するときのへ平均変化率は以下のように求められます。
$$ \large{ \frac{(y2-y1)}{(x2-x1)} }$$
これは「yの差分」を「xの差分」で割った値です。これにより、xが1動いた時のyの変化度を求められるわけです。例えば(1,1)と(3,5)の平均変化率は↓になります。
xが1動くと、yが2動くわけですね。
関数上の平均変化率
上の平均変化率の考えを関数上の値で考えます。関数上のyはy=f(x)で表せるため、平均変化率は以下のように表せます。
$$ \large{ \frac{(f(x2)-f(x1))}{(x2-x1)} }$$
x1,x2という適当な2点を選べば、平均変化率を求める事が出来るわけです。
実際に関数上の2点の平均変化率を調べてみよう!
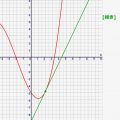
上記の考えの理解を深めるため、適当な三次関数上で2点の変化率が計算できるシミュレーターを作ってみました!
↓のx1,x2を変化させると、自動的に平均変化率を求めます。さらにグラフ上にその2点を結ぶ線を描画します。色々値を変えてみて下さい!
\( {\displaystyle \frac{(f(x2)-f(x1))}{(x2-x1) } =} \) ((+ 1) – (+ 1))÷((+ 1) – (+ 1))= + 1
上の2点を結ぶ線を\(y=ax+b\)とすると、そのaは平均変化率そのものです。このa=平均変化率をこの線の「傾き」といいます。この「線の傾き」を微分では求めていくんです!
微分=「各点での接線の傾きを求める」
上で説明した「平均変化率」「傾き」を使って、以下のように微分の定義をすることが出来ます。
関数f(x)の、各点での接線の傾きを表す関数f'(x)を求めること
そして接線の定義は以下の通りです。
x1近くでの関数上の平均変化率の直線、平均変化率の定義のx2をx1に限りなく近づけた時にできる線
平均変化率はx1,x2の2点が定義に必要ですが、究極的にx2を限りなくx1に近づけて、x1付近での平均変化率を計算しようとするのがこの「接線」という考え方です。例えば、x1=1,x2=3だった場合にx2を3→1に限りなく近づいて行った時に出来る線が接線であり、その平均変化率が「接線の傾き」です。分かりにくいので、↓のシミュレーターを用意してみました!
x1での接線を求めるシミュレーター
このシミュレーターではx1を指定すると、少し先にx2が配置されます。このx2が段々とx1に近づいていき、最終的に接線が求まる過程をアニメーションで見ることが出来ます。
平均変化率の考えから、接線が決まる過程をこのアニメーションで理解しましょう!
この過程で求められる「傾き」(平均変化率)をx1での「微分係数」と言います。
微分(導関数)の定義
点x1での微分係数(接線の傾き)の求め方
上記の説明/イメージは、2点x1,x2を使って以下の式で表すことが出来ます。
$$ \large{ \displaystyle \lim_{ x2 \to x1 } \frac{f(x2) – f(x1)}{x2-x1} }$$
limという記号は、「x2をx1に限りなく近づけるよ」という意味です。x1とx2の平均変化率の式に対して、x2→x1に限りなく近づけた時の値を計算すると「接線の傾き」が求められるわけです。
ここでx1とx2の差分をhとすれば、\( h = x2-x1 \)と表せるので、上記式は
\( \displaystyle \lim_{ x2 \to x1 } \frac{f(x2) – f(x1)}{x2-x1} \)
\(= \displaystyle \lim_{ h \to 0 } \frac{f(x1+h) – f(x1)}{h} \)
という形に変形出来ます。上記式を計算し、hを0に近づけていけば「x1での接線の傾き(微分係数)」が求められるわけです。これは「x1周辺でどれぐらい平均変化率があるか」を極限的にhの幅を小さくしていって求めた値です。
導関数(微分)の求め方
上の定義は点x1での接線の傾きの求め方でした。これを拡張し、任意の点xでの接線の傾きを求める関数を考えます これは単純に上記の式をx1→xとして一般化するだけです。これを導関数といいます。導関数は関数fにf’をつけて表すことが慣習的になっています。
$$ \large{ f'(x) = \displaystyle \lim_{ h \to 0 } \frac{f(x+h) – f(x)}{h} }$$
一度導関数f'(x)を求めてしまえば、ここにxの値を代入することで各点での接線の傾きが求められるわけです。そしてこの導関数を求めることこそ、微分なのです!
では、この導関数どのように求めていくのでしょうか?分母に0に向かうhがあるので、計算できないのでは??って思ってしまいますが、ちゃんと値を当てはめていけば計算可能なのです!この導関数の具体的な求め方については、次の記事で説明させて頂きます!
補足:微分の別表現
上記ではf(x)の微分・導関数をf'(x)として表現しました。この導関数の表し方は別の表現方法もあります。
xで微分で明に示すために↓のようにdy,dxを使って↓のように表すこともあるんです。
$$ \large{ f'(x) = \displaystyle \frac{dy}{dx} = \frac{d f(x)}{dx} }$$
dxとは微小量のxという意味です。\(\Large{\frac{dy}{dx}}\)と書くことで、微小量の変化dy,dxの傾きを計算することを表しているわけです!
⇒「微分の基礎」カテゴリ記事一覧
その他関連カテゴリ