ドップラー効果(音源の移動の影響)をシミュレーターで確かめよう！[物理入門]

2021-07-11　 ドップラー効果

本ページでは物理の「ドップラー効果(音源の移動の影響)」をシミュレーターを用いて分かりやすく解説します！

音源と観測者の「振動数」は異なる(おさらい)

今まで波の振動数(周波数)について、解説してきましたが、厳密にいうと振動数は「音源側」と「観測者側」の2つの意味合いがあります。

この2つは、音源者と観測者が動いていなければ同一です。しかし、音源や観測者が異なっている場合、この2つは異なってきます。「受信する振動数(周波数)」こそ、人間が感じる音であるため、聞こえ方が変わってくるという事なんです。これがドップラー効果の原理です！

「音源の移動の影響」を求める

前回の考察の通り、「音源の移動」により、音波の疎密が変化します。つまり、波長・振動数が変化します。

この時の波長と振動数の変化は↓の式で求められます。

なぜならば、↓の図のように、1秒間で音波と音源が離れる距離は「\(v – v_s\)」になるからです。

↓のように本来はvの間にf個の波があったのに、\(v – v_s\)の間にf個の波がある状態に圧縮されます。

[元の波]

[圧縮された波]

1秒間に発信する周期数は同じであるため、波長は\(\LARGE{\frac{v \ – \ v_s}{v}}\)倍に圧縮されるわけです！

また、音速vは変わらないため、逆に振動数は\(\LARGE{\frac{v}{v \ – \ v_s}}\)倍されるわけです。

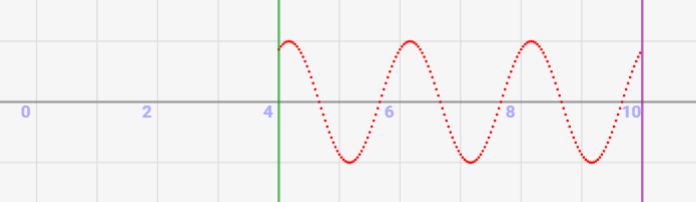
「ドップラー効果(音源の移動の影響)」をシミュレーターで確認しよう！

このシミュレーターでは、音源の速度によって、観測する振動数が変わることを確かめられます！

結果の考察

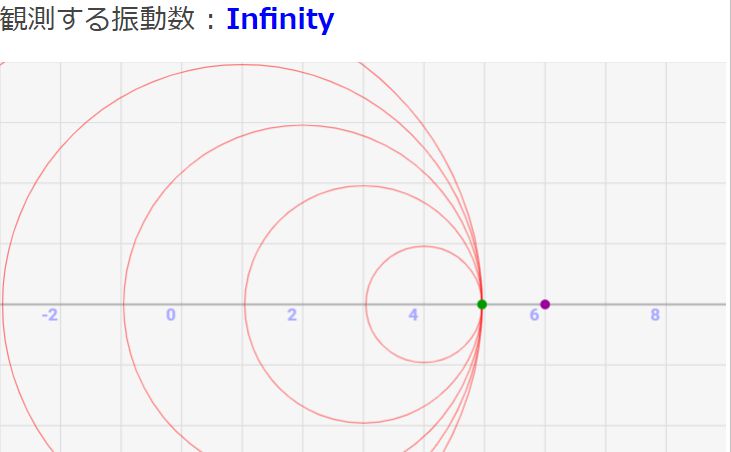
音源が音速に近づくほど振動数は大きくなっていく

シミュレーターで音源の速度を上げていくと、公式通り、振動数が大きくなっていくことが分かると思います。

音速に近い場合、↓のように短い区間に多くの波が密集するため、高い振動数となります。

特に音源が音速と一致した場合、↓のように1区間に無限の波が密集します。これが、音速を超える時に発生する衝撃波の正体です。

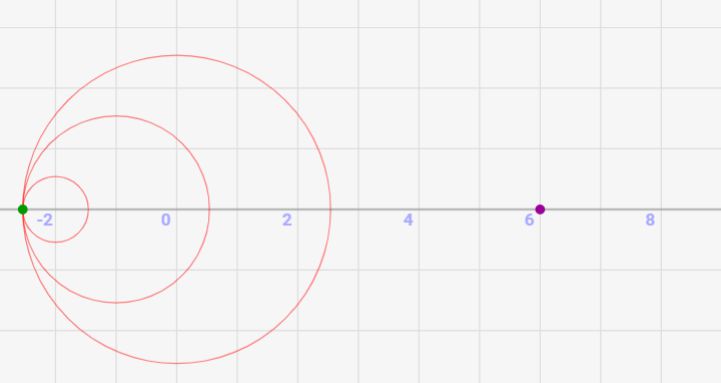
音源が反対方向にいくと、振動数は小さくなっていく

上記結果と逆で、反対方向に音源が移動すると、波が疎となり、観測点での振動数は小さくなっていきます。

　
　
次回は、「観測者が移動することの影響」について考察していきます
　

[関連記事] 音波

1．横波・縦波

2．音速

3．音の「大きさ・高さ・音色」の決まり方

4．音叉(おんさ)の「うなり」

5．ドップラー効果の原理

6．ドップラー効果(音源の移動の影響)(本記事)

7．ドップラー効果(観測者の移動の影響)

8．ドップラー効果(総合)