「DIE WITH ZERO(ゼロで死ね)」の価値観を数値シミュレーション化!数値実験で、その考え方の理解を深めよう!
目次
書籍「DIE WITH ZERO(ゼロで死ね)」の考え方とは?
この本の主な考え方は、コチラのページで紹介していますので、ここでは概要だけおさらいしておきます。
老後のために、多くの人が貯金を貯め込んだりしています。しかし、老後のために、若い時に我慢してまで多くのお金を貯め込むのはどうなのか?と疑問を呈しているのがこの本の特色です。
この本では「年を追うごとに出来ることが少なくなっていき、お金を投資して得られる幸福が減っていくこと」「最終的に貯金ゼロで死ねるように、残り時間を意識して、計画的にお金を消費していくこと」が大事だと述べられています。
この考え方、、自分の考え方に似ていて凄く共感しました!そして、経済学の効用を用いれば、うまく数式モデル化してシミュレーション化できると考えました!
ということで、「如何に若い時から計画的にお金を消費することが大事か」を示すために、シミュレーション化してみました!コレを使うと、どの世代でどれぐらいお金を使うのが最適なのか、シミュレーターで実験ができます!是非チャレンジしてみて下さい!
「DIE WITH ZERO(ゼロで死ね)」的思考 シミュレーションの前提条件
このシミュレーションを行う前に、多くの前提を述べておく必要があるので列挙させて頂きます!
前提0: シミュレーション条件の設定
まず前提として↓のようなシミュレーション条件を設定します。これは今回の主題である「DIE WITH ZERO(ゼロで死ね)の価値観を理解する」ため、余計な条件を削ぎ落とすためです。
前提
- 自由にお金を使えて自分で稼ぐ20歳からのシミュレーション
- 80歳で死ぬ前提
- 各年代10歳ごと区切って計算
- 給与取得期間は20歳~59歳までとする
- 借金は出来ないものとする
- その他、ローン無し年金無し
このような前提になります。まず簡単のために10歳ごとに分けて、投資できるようにします。そして、20~80歳でのシミュレーションとします。20歳未満で自分でお金動かせる人も少ないと思うので除外します。給与については後述しますが、20歳~59歳の間のみ貰えるものとしました。また、ローン・借金・年金などは考慮外です。
可能な限り、現実に合わせたいのですが、複雑な計算式になると、理解が難しくなるのでこのような前提にしています><
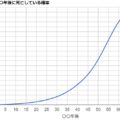
前提1: 効用(幸福度)関数は年齢が増えるごと減衰していく
これは「DIE WITH ZERO(ゼロで死ね)」で解説した考え方ですね。効用は年齢ごとに減っていくという前提です。
式としては↓を用います。
効用減少度によって、効用がどれぐらい減少するかを調整できます。効用減少度=1が全く効用が変わらない場合であり、0に近づくほど年齢による減少度が大きくなっていきます。
↓効用減度を上下させて確認してみて下さい
前提2: 効用増加率は投資するごとに減少していく
一般的に、投資額を10倍にしたら効用が10倍になるということはありません。コチラの記事で解説していますが、効用増加率は投資額が増えるごとに下がっていきます。ですので、その関係性を表すために↓のモデル式を用います。ルートになってますので、投資してくほど効果が下がっていくことを意味しています。
↓グラフにするとこんな感じです。投資額が増えるほど、効用は伸びなくなってきます
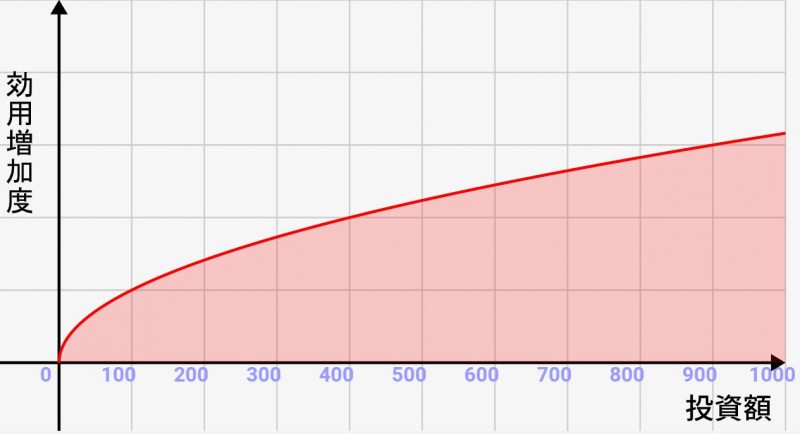
そして、この効用増加度と上記の年齢による効用の減少率を掛け合わせた関数を、最終的に用いる効用関数とします。
\(効用 = 効用減度^{年齢} × \sqrt{その年齢での投資額}\)
この関数を20~80歳で足して、その総和を最大化させる問題とします。つまり、↓が総合効用とします
\( \displaystyle 総合効用 = \sum_{年齢=20}^{80} 効用減度^{年齢} × \sqrt{その年齢での投資額}\)
前提3: 年収は500万ベースで、勤務年数比例で増加する
とりあえずあまり変数が多いとややこしくなるので、年収は500万円固定で、そこから勤務年数に比例して年収が増加していくモデルを採ります。
式で表すと↓のような感じです。設定した年収増量ごと年収が増えていきます。給与増度=0で、ずっと500万固定になります。
\(年収 = (年齢 – 20) × 年収増量 + 500\)
↓年収増量を上下させて設定給与を確認してみて下さい
借金は出来ない前提ですので、この金額の範囲で投資していく事を考えます。
「DIE WITH ZERO(ゼロで死ね)」的思考 シミュレーション
上記の前提で、各世代で投資していったとき、効用値(幸福度)がどのような値になるのかをシミュレーションで実験できます!どのような場合に効用が最大化するのか実験して確認してみましょう!
前提条件設定
上記の説明参照。デフォルトのままで構いません!
シミュレーション
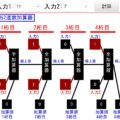
↓矢印で示している世代に何百万円投資するか決めて、「投資」ボタンを押して下さい!20代~70代まで投資が終わる完了です。
残金をチェックしながら、投資額を配分し、出来る限り大きな効用になるようにチャレンジしてみて下さい!
投資額(百万単位)
現合計効用:0
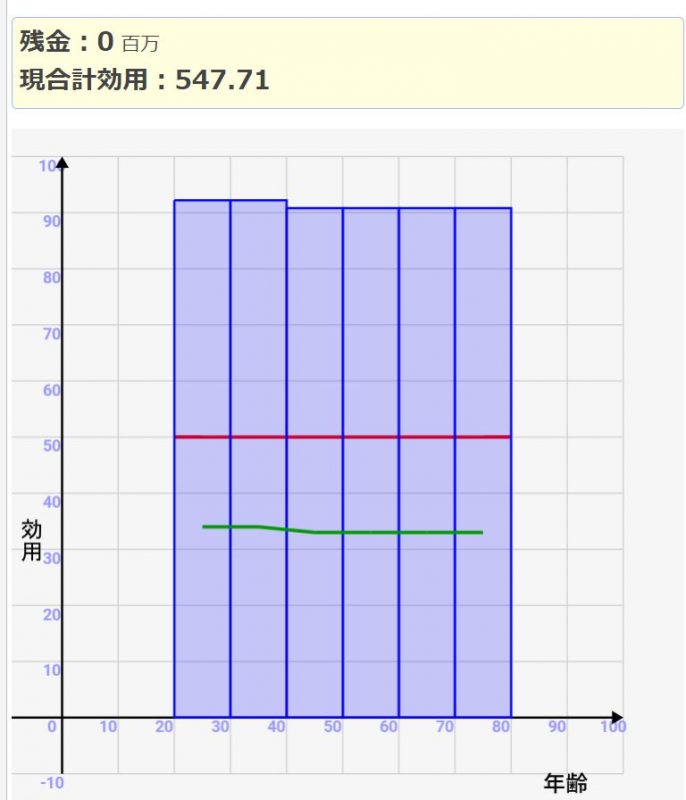
* 投資で得られた効用を青棒グラフで示しています
* 各世代での投資額を緑線で示しています。
* 各年代での効用関数減少を示した値を赤線で示しています。この値が高い世代ほど、同じ投資額でも効用が高くなるという意味です
シミュレーション結果考察
上記のシミュレーターは設定パラメタによって、最適解が大きくことなってきますが、その中でも↓のような特徴があります。
ここでは簡単のため、年収増量=0、つまり各年で500万円ずつ得られる場合で考察していきます。
効用が世代によって変わらない場合は、全年代で同額投資したときが最大効用となる
今回のシミュレーションの場合、効用減度=1の場合に全年代で効用の上がり方が同じになります。この場合は、全世代で全く同じ額を投資する↓のパターンが最大になります。
年をとっても幸せになれるなら、同じぐらいずつ使うのが一番良いということですね!
年を取るごとに、効用が減少する場合は、若いうちに多く使ったほうが効用が上がる
これは当たり前のことですが、効用関数が分かり世代のほうが高い値をとりやすいので、平等に投資したり、年をとってから使うよりも、若いうちに投資してしまったほうが効用が得られやすくなります。
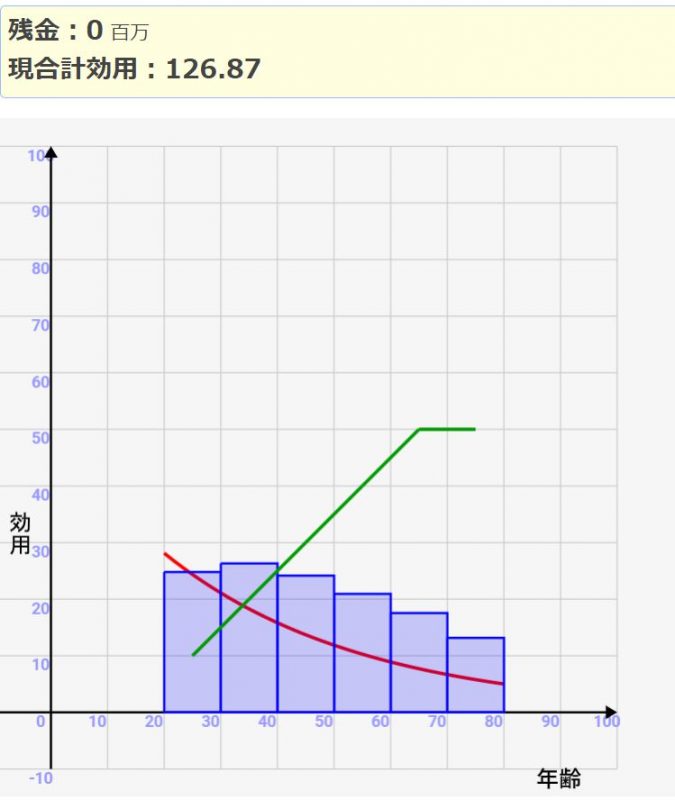
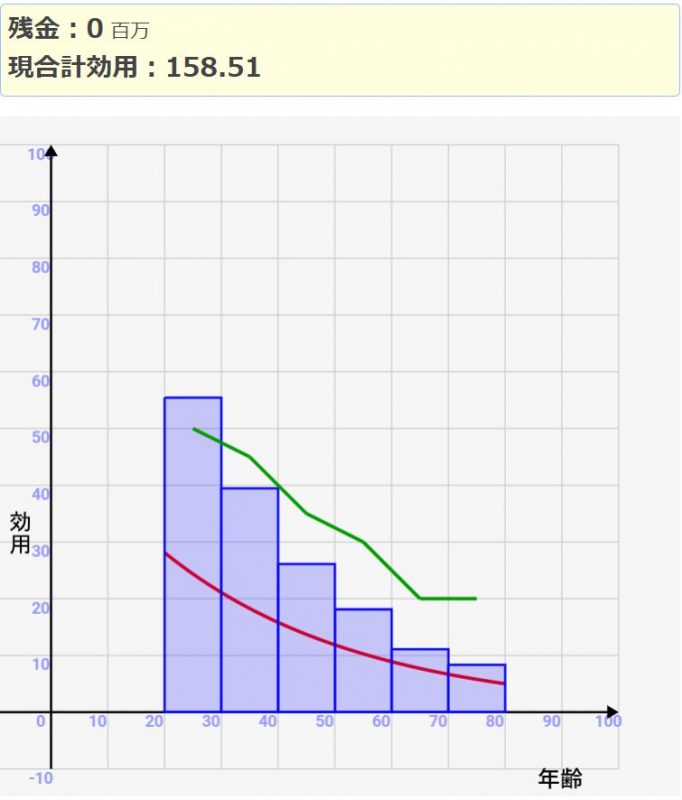
このようにいつお金を投資するかによって、効用が大きくかわります。年をとってから使う場合は120台ですが、効率よく若い時期に投資すると160程度まで伸びます。
こう考えると、不安だからといって、分かり時期に無理して貯め込むのも絶対に正しいとは言えませんよね。将来のために我慢することが正しいわけではないんです!
確かに若い時に投資したほうが効率良いが、使い果たすのが正解でない
上記の実験結果のとおり、若い時に多めにお金を使うのが良さそうに見えます。しかし、出来る限り若い時期にお金を最大限使うのが最適ではありません。
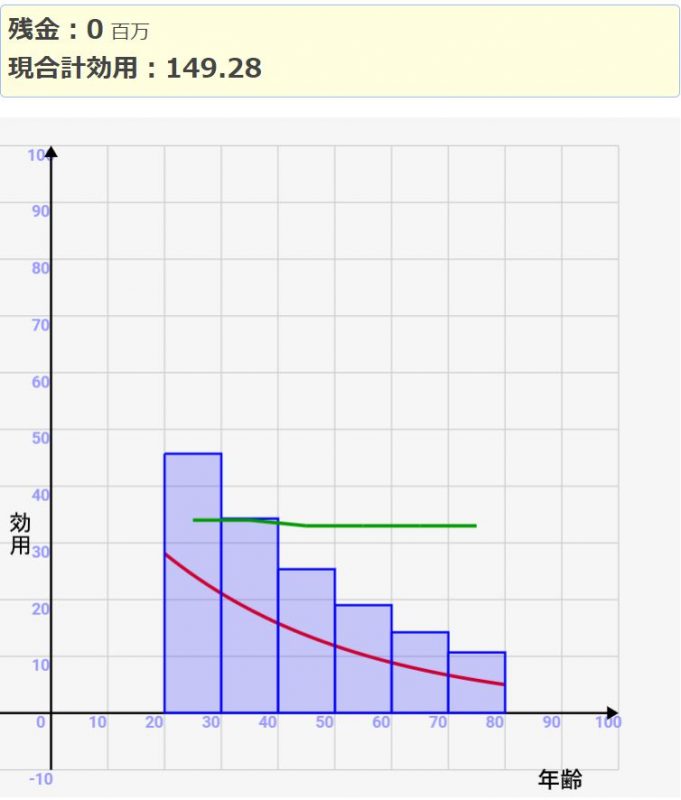
↓若い時に出来るだけ使うようにした場合。上記の最適な場合より効用が落ちます。
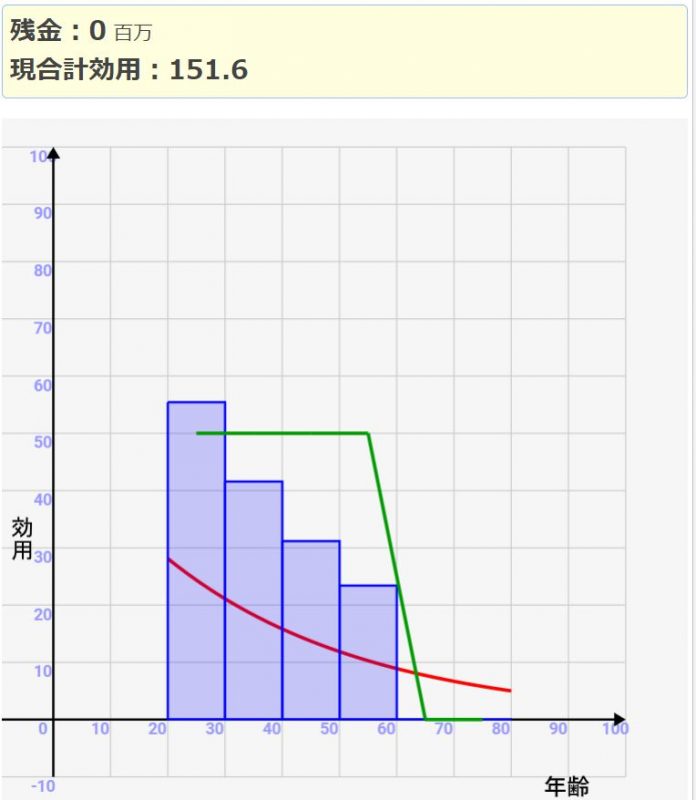
上記で説明した「年収/投資額が増えるほど、効用の上げ幅は下がっていく」という性質があるので、若い時に多く使いながら、それでもバランスよく配分して投資していく必要があるんです。難しいですね><
世代による効用の差が激しくなるほど、若い時に消費したほうが効用が高くなる
歳をとると、どれぐらい効用が下がっていくのかは人によると思います。ただ、その効用の落ち方が激しい場合は、出来る限り早い世代でお金を使いきったほうが効用が大きくなります。
とにかくある30代ぐらいまでは得られたお金を全て投資し、以後は少しずつ分散して投資するような使い方が効用最大になります。もっというと、少々の利息はあったとしても、借金してでも先行投資して先につかったほうが効用が高くなります。
さすがにここまで無理することはないと思いますが、それぐらい若い時が大事っていうことですね。
↓世代間の効用の差が激しいと、老後にお金をとっておく意味が薄れていく
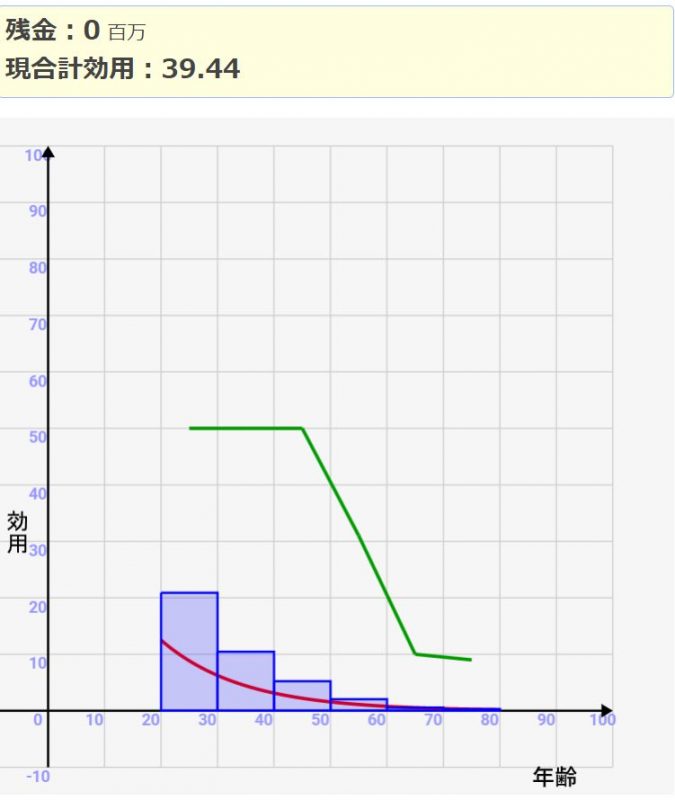
まとめ:自分の効用関数の減少率を想定して最適な投資プランを!我慢して老後のために貯め込むのは絶対的に良いとは言えません!
ちょっと複雑な話になりましたが、まとめです。
上記の通り、モデルによって、どのようなパラメタをとるかで最適な投資配分は変わってきます。効用関数がどのように年をとると減少するかにより、いつお金を使うのが最適なのかが変わってきます。
ただ、一般論として、若い時ほど色んなことができるため、同額の投資でも幸福度(効用)が得られやすい傾向は確実にあると思います。そうなると、、、上記のように、数学的には早めに(かつそれでもバランスよく)投資をしたほうが効用最大化になります。
老後の不安とか、子供への投資とか色々事情はありますが、、、我慢して貯金することが絶対正ではないというのは事実だと思います。
老後のために、老後のためにと我慢して過ごしてたら、使いきれずに人生終わってしまった、、、そうなるのは悲しいですよね><
そうなるためにも、「ゼロで死ぬ」ためにも、若い時から計画的に投資/消費していくのが重要なのではないでしょうか!!

⇒「経済学/投資」カテゴリ記事一覧
その他関連カテゴリ